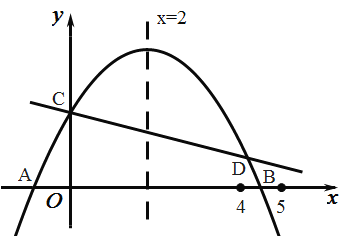题目内容
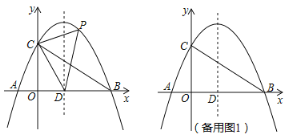
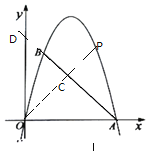
【题目】如图,抛物线![]() 过
过![]() ,
,![]() 两点.
两点.
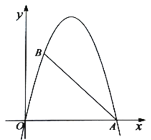
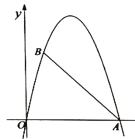
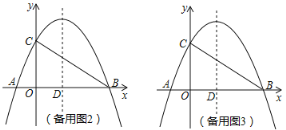
备用图1 备用图2
(1)求该抛物线的解析式;
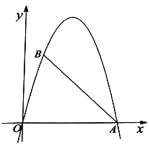
(2)点![]() 是抛物线上一点,且位于第一象限,当
是抛物线上一点,且位于第一象限,当![]() 的面积为6时,求点
的面积为6时,求点![]() 的坐标;
的坐标;
(3)在线段![]() 右侧的抛物线上是否存在一点
右侧的抛物线上是否存在一点![]() ,使得
,使得![]() 分
分![]() 的面积为
的面积为![]() 两部分?存在,求出点
两部分?存在,求出点![]() 的坐标;不存在,请说明理由.
的坐标;不存在,请说明理由.
【答案】(1)抛物线的表达式为:![]() ;(2)点
;(2)点![]() 的坐标为:
的坐标为:![]() 或
或![]() ; (3)点
; (3)点![]() 的坐标为
的坐标为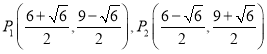 .
.
【解析】
(1)根据抛物线y=ax2+bx过A(5,0),B(1,4)两点,可以求得该抛物线的解析式;
(2) 过点![]() 作直线
作直线![]() 轴交
轴交![]() 点
点![]() ,设
,设![]() ,则
,则![]() ,分当点
,分当点![]() 在
在![]() 上方时和当点
上方时和当点![]() 在
在![]() 下方时,列方程求解即可;
下方时,列方程求解即可;
(3) 设![]() 交
交![]() 于点
于点![]() ,分当
,分当![]() 或
或![]() 时,由三角形相似,列方程求解即可.
时,由三角形相似,列方程求解即可.
(1)将点![]() 的坐标代入抛物线表达式,
的坐标代入抛物线表达式,
得:![]() ,
,
解得:![]() ,
,
所以抛物线的表达式为:![]()
(2)求得直线![]() 的表达式为:
的表达式为:![]() ;
;
过点![]() 作直线
作直线![]() 轴交
轴交![]() 点
点![]() ,如图,
,如图,
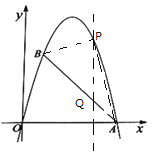
设![]() ,
,
则![]() .
.
当点![]() 在
在![]() 上方时,
上方时,
![]() ,
,
![]() ,
,
解得![]() ,
,
即![]()
当点![]() 在
在![]() 下方时,
下方时,
![]() ,
,
![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
即![]()
综上,点![]() 的坐标为:
的坐标为:![]() 或
或![]() ;
;
(3)由(2)得直线![]() 的表达式为:
的表达式为:![]() ;
;
令![]() ,则
,则![]() ,
,
即直线![]() 交
交![]() 轴于点
轴于点![]() .
.
设![]() 交
交![]() 于点
于点![]() ,如图,
,如图,
当![]() 或
或![]() 时,
时,
则![]() 分
分![]() 的面积为
的面积为![]()
![]() 轴交
轴交![]() 点
点![]() ,
,
![]() ,
,
![]() .
.
①当![]() 时,
时,![]() ,
,
由(2)得:![]() ,
,
即![]() ,
,
解得![]() ,
,
即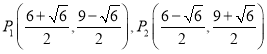 .
.
②当![]() 时,
时,![]() ,
,
由(2)得:![]() ,
,
即![]() ,所得方程无解.
,所得方程无解.
综上所述:点![]() 的坐标为
的坐标为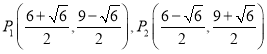 .
.

练习册系列答案
相关题目
【题目】某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位),损坏的苹果约有______kg.