题目内容
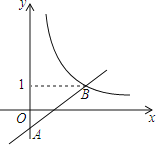
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 轴,
轴,![]() ,抛物线
,抛物线![]()
![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .
.
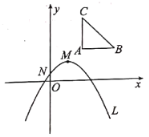
(1)设![]() 为
为![]() 中点,直接写出直线
中点,直接写出直线![]() 的函数表达式:______________.
的函数表达式:______________.
(2)求点![]() 最高时的坐标;
最高时的坐标;
(3)抛物线有可能经过点![]() 吗?请说明理由;
吗?请说明理由;
(4)在![]() 的位置随
的位置随![]() 的值变化而变化的过程中,求点
的值变化而变化的过程中,求点![]() 在
在![]() 内部所经过路线的长.
内部所经过路线的长.
【答案】(1)![]() ;(2)点
;(2)点![]() 最高时的坐标为
最高时的坐标为![]() ;(3)不可能,理由详见解析;(4)点
;(3)不可能,理由详见解析;(4)点![]() 在
在![]() 内部所经过路线的长为
内部所经过路线的长为![]() .
.
【解析】
(1)由题意,A点的横纵坐标相等,P点的横纵坐标相等,可得直线AP为y=x;
(2) ![]() 中令x=0,得出y关于t的二次函数,根据二次函数的性质得出最大值即可;
中令x=0,得出y关于t的二次函数,根据二次函数的性质得出最大值即可;
(3)先求出C点的坐标,将C点坐标代入二次函数解析式,得出关于t的一元二次方程,再根据一元二次方程判别式的正负判断;
(4)由![]() ,知顶点
,知顶点![]() ,所以点M在
,所以点M在![]() 内部所经过路线的长即为AP的长.
内部所经过路线的长即为AP的长.
解:(1)∵![]() ,
,![]() ,
,![]() 轴,
轴,![]() ,
,
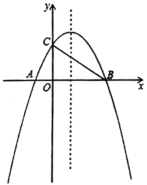
∴点B的坐标为(4,2),点C的坐标为(2,4),
又P为BC的中点,∴点P的坐标为(3,3),
∴由A,P两点的坐标可得直线AP的解析式为![]() .
.
故答案为:y=x.
(2)当![]() 时,
时,
![]()
![]()
![]()
最大值为![]() ,即与
,即与![]() 轴交点纵坐标的最大值.
轴交点纵坐标的最大值.
![]() 点
点![]() 最高时的坐标为
最高时的坐标为![]() .
.
(3)不可能.
理由:把![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,化简为
,化简为![]() .
.
![]() ,
,
![]() 方程没有实数根,即抛物线不可能经过点
方程没有实数根,即抛物线不可能经过点![]() .
.
(4)由![]() ,知顶点
,知顶点![]() ,
,
![]() 在
在![]() 的位置随
的位置随![]() 的值变化而变化的过程中,
的值变化而变化的过程中,
点![]() 都在直线
都在直线![]() 上移动,且经过直线
上移动,且经过直线![]() 上的点
上的点![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,![]() .
.
![]() 点
点![]() 在
在![]() 内部所经过路线的长为
内部所经过路线的长为![]() .
.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目