题目内容
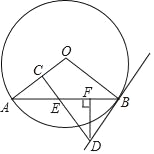
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,过D点作DF⊥AB于点F,
①则cos∠EDF= ;
②求⊙O的半径.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]()
【解析】分析:(1)欲证明DB=DE,只要证明∠DEB=∠DBE;
(2)①连接OE,有线段垂直平分线的性质,可得EF=BE=3,
在Rt△DEF中,由勾股定理DF=4,则cos∠EDF=![]() =
=![]() ;
;
②只要证明∠AOE=∠DEF,可得sin∠DEF=sin∠AOE=![]() ,由此求出AE即可解决问题.
,由此求出AE即可解决问题.
详解:(1)∵BD为切线,
∴OB⊥BD,
∴∠OBD=90°,即∠OBE+∠DBE=90°,
∵CD⊥OA,
∴∠A+∠AEC=90°,
而OA=OB,
∴∠A=∠OBE,
∴∠AEC=∠DBE,
∵∠AEC=∠DEB,
∴∠DEB=∠DBE,
∴DB=DE;
(2)①连接OE,如图,
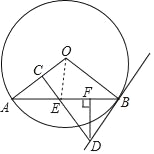
∵E是AB的中点,
∴AE=BE=6,
∵DE=DB=5,DF⊥BE,
∴EF=BE=3,
在Rt△DEF中,DF=![]() =4,
=4,
cos∠EDF=![]() =
=![]() ;
;
故答案为![]() ;
;
②连接OE,
∵E是AB的中点,
∴OE⊥AB,
∴∠OEB=90°
∴∠EOB+∠EBO=90°,
而∠OBE+∠DBE=90°,
∴∠EOB=∠DBF,
在Rt△OBE中,sin∠EOB=![]() =sin∠DBF=
=sin∠DBF=![]() ,
,
∴OB=![]() =
=![]() ,
,
即⊙O的半径为![]() .
.

【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为![]() (分),且
(分),且![]() ,将其按分数段分为五组,绘制出以下不完整表格:
,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩 | 频数(人数) | 频率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 。