题目内容
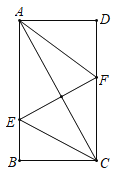
【题目】如图，在矩形ABCD中，AD=2，AB=4，E、F分别是AB、CD边上的动点，EF⊥AC，则AF+CE的最小值为________．
【答案】5
【解析】
如图（见解析），先根据平行四边形的判定与性质得出
，再根据两点之间线段最短得出
确定最小值时，点F的位置，从而可得最小值为
长，然后根据矩形的判定与性质、相似三角形的判定与性质可得
，从而可求出EF的长，最后在
中，利用勾股定理即可得．
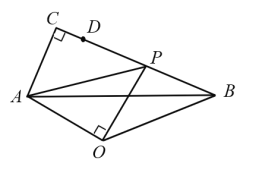
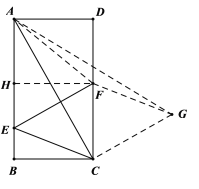
如图，过点F作
于点H，分别过点F、C作CE、EF的平行线，两平行线相交于点G，连接AF、AG
则
四边形CEFG是平行四边形
由两点之间线段最短可知，当点
共线时，取得最小值，最小值为
即
的最小值为
四边形ABCD是矩形，
，
，
，四边形BCFH是矩形
在
和
中，
，即
解得
又
，即
则在中，
即的最小值为5
故答案为：5．
练习册系列答案
阅读快车系列答案
相关题目
