题目内容
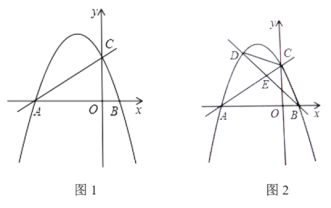
【题目】如图1,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,二次函数y=
x+2与x轴交于点A,与y轴交于点C,二次函数y=![]() x2+bx+c的图像经过A、C两点,与x轴的另一交点为点B.
x2+bx+c的图像经过A、C两点,与x轴的另一交点为点B.
(1)求二次函数的表达式;
(2)当m≤x≤m1时,二次函数y![]() x2bxc的最大值为2m,求m的值;
x2bxc的最大值为2m,求m的值;
(3)如图2,点D为直线AC上方二次函数图像上一动点,连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1,△BCE的面积为S2,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意得到![]() ,
,![]() 代入
代入![]() ,于是得到结论;
,于是得到结论;
(2)先求抛物线的对称轴,然后分m+1≤![]() ,m<
,m<![]() <m+1,m>
<m+1,m>![]() 三种情况,利用二次函数的图象及性质可以分别求出m的值.
三种情况,利用二次函数的图象及性质可以分别求出m的值.
(3)如图,过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴交于
轴交于![]() 于
于![]() ,构造
,构造![]() ,利用相似三角形的性质得
,利用相似三角形的性质得![]() ,由DM长得二次函数即可解答.
,由DM长得二次函数即可解答.
解:(1)![]() 直线
直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,
![]() 抛物线
抛物线![]() 经过
经过![]() .
.![]() 两点,
两点,
![]()
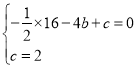 ,
,
![]()
 ,
,
![]() 抛物线的函数表达式为
抛物线的函数表达式为![]() ;
;
(2)在![]() 中,对称轴为x=
中,对称轴为x=![]() ,当m≤x≤m1时,二次函数y
,当m≤x≤m1时,二次函数y![]() x2bxc的最大值为2m,有三种可能:
x2bxc的最大值为2m,有三种可能:
I.若m+1≤![]() ,即m≤
,即m≤![]() 时,当x=m+1时,函数有最大值-2m,
时,当x=m+1时,函数有最大值-2m,
∴![]() ,
,
解得,![]() ,
,![]() ,(均不合题意,舍去)
,(均不合题意,舍去)
II.若m<![]() <m+1,即
<m+1,即![]() <m<
<m<![]() 时,当x=
时,当x=![]() 时,函数有最大值为
时,函数有最大值为![]() ,
,
即![]() ;解得:
;解得:![]()
III.若m>![]() ,当x=m时,函数有最大值为-2m,
,当x=m时,函数有最大值为-2m,
∴ ![]() ,
,
解得,![]() ,
,![]() ,
,
综上所述,m的值为![]() 或
或![]() 或
或![]() .
.
(3)令![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
如图1,过![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,
,
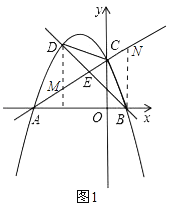
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 当
当![]() 时,
时,![]() 的最大值是
的最大值是![]() ;
;

【题目】为进一步提升学生体质健康水平,我市某校计划用400元购买10个体育用品,备选体育用品及单价如表:
备用体育用品 | 足球 | 篮球 | 排球 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买足球和排球共10个,则足球和排球各买多少个;
(2)若学校先用一部分资金购买了a个排球,再用剩下的资金购买了相同数量的足球和篮球,此时正好剩余30元,求a的值.