题目内容
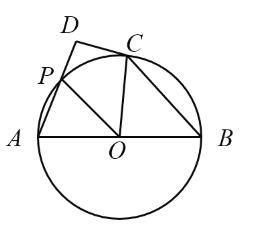
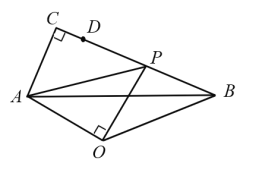
【题目】如图,![]() 中,
中,![]() 点
点![]() 是
是![]() 边上一点,
边上一点,![]() 点
点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰
的下方作等腰![]() 连接
连接![]() 当
当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止的过程中,
停止的过程中,![]() 面积的最大值等于_____________________
面积的最大值等于_____________________![]()
【答案】![]()
【解析】
设![]() ①当
①当![]() 时,作
时,作![]() 于
于![]() 于
于![]() .先证明
.先证明![]() ,进而可得四边形
,进而可得四边形![]() 是正方形;设
是正方形;设![]() ,用x、y表示出PB和OH,然后运用三角形的面积公式二次函数求最值即可;②当
,用x、y表示出PB和OH,然后运用三角形的面积公式二次函数求最值即可;②当![]() 时,同理(1)可得
时,同理(1)可得![]() ,根据二次函数的性质可得,当x=4时有最大值.然后比较即可确定最大值.
,根据二次函数的性质可得,当x=4时有最大值.然后比较即可确定最大值.
解:设![]()
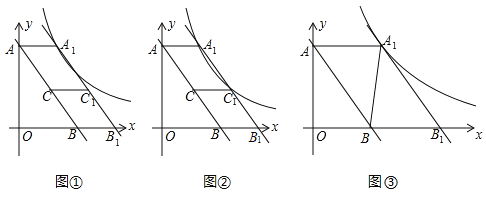
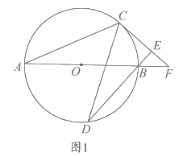
①如图1,当![]() 时,作
时,作![]() 于
于![]() 于
于![]() .
.
∴∠OHP=∠OGA=90°
∵四边形AOPC中,∠C=90°,∠AOP=90°
∴∠CAB+∠OPC=180°
∵∠BPO+∠OPC=180°
∴∠OPH=∠OAG
∵在△AOG和△POH
∠OHP=∠OGA,∠OPH=∠OAG,AO=OP
∴![]() ,
,
∴OH=OG
∵∠OHP=∠OGA=∠C=90°
∴四边形![]() 是正方形
是正方形
设![]() ,则
,则![]() ,得
,得![]() ,即有
,即有![]() .
.
∴![]()
∴![]()
所以当![]() 时,
时,![]()

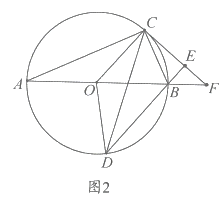
②如图2,当![]() 时,同理可得
时,同理可得![]()
所以当x=4时,![]()
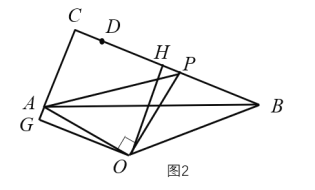
综上,当![]() 时,
时,![]() .
.

练习册系列答案
相关题目
【题目】绘制函数![]() 的图象,我们经历了如下过程:确定自变量
的图象,我们经历了如下过程:确定自变量![]() 的取值范围是
的取值范围是![]() ;列表-描点--连线,得到该函数的图象如图所示
;列表-描点--连线,得到该函数的图象如图所示
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
观察函数图象,回答下列问题:
(1)函数图象在第 象限;
(2)函数图象的对称性是
B.只是轴对称图形,不是中心对称图形
A.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
C.不是轴对称图形,而是中心对称图形
(3)在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
(4)方程![]() 是否有实数解?说明
是否有实数解?说明