��Ŀ����
��֪����ͼ����A��y�ύ��C��D���㣬Բ��A������Ϊ��1��0������A�İ뾶Ϊ
������C����A�����߽�x���ڵ�B��-4��0����
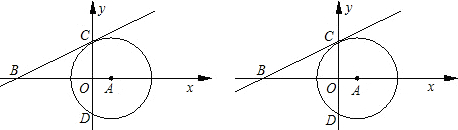
��1��������BC�Ľ���ʽ��
��2������P�ǵ�һ�����ڡ�A�ϵ�һ�㣬����P����A��������ֱ��BC�ཻ�ڵ�G���ҡ�CGP=120�㣬���G�����ꣻ
��3�������ƶ���A��Բ��Aʼ�ձ�����x���ϣ�����ֱ��BC����E��F�����ƶ��������Ƿ���ڵ�A��ʹ��AEF��ֱ�������Σ������ڣ������A�����ꣻ�������ڣ���˵�����ɣ�
| 5 |

��1��������BC�Ľ���ʽ��
��2������P�ǵ�һ�����ڡ�A�ϵ�һ�㣬����P����A��������ֱ��BC�ཻ�ڵ�G���ҡ�CGP=120�㣬���G�����ꣻ
��3�������ƶ���A��Բ��Aʼ�ձ�����x���ϣ�����ֱ��BC����E��F�����ƶ��������Ƿ���ڵ�A��ʹ��AEF��ֱ�������Σ������ڣ������A�����ꣻ�������ڣ���˵�����ɣ�
��1����ͼ1��ʾ������AC����AC=
��
��Rt��AOC��AC=
��OA=1����OC=2��
���C��������0��2����
������BC�Ľ���ʽΪy=kx+b��������C��0��2����B��-4��0����
����
����֮��
��
��y=
x+2����4�֣�
��2����ͼ1��ʾ�����G������Ϊ��a��c��������G��GH��x�ᣬ����ΪH�㣬
��OH=a��GH=c=
a+2����5�֣�
����AP��AG��
��ΪAC=AP��AG=AG������Rt��ACG��Rt��APG��HL����
���ԡ�AGC=
��120��=60�㣬
��Rt��ACG�У���AGC=60�㣬AC=
��
��sin60��=
����AG=
����6�֣�
��Rt��AGH��AH=OH-OA=a-1��GH=
a+2��
��AH2+GH2=AG2��
�ࣨa-1��2+(
a+2)2=(
)2��
��֮�ã�a1=
��a2=-
����ȥ������7�֣�
���G��������
��
+2������8�֣�
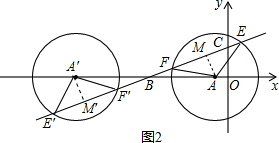 ��3����ͼ2��ʾ�����ƶ������У����ڵ�A��ʹ��AEFΪֱ�������Σ���9�֣�
��3����ͼ2��ʾ�����ƶ������У����ڵ�A��ʹ��AEFΪֱ�������Σ���9�֣�
Ҫʹ��AEFΪֱ�������Σ���AE=AF��
���AEF=��AFE��90�㣬��ֻ���ǡ�EAF=90�㣻
��Բ��A�ڵ�B���Ҳ�ʱ������A��AM��BC������Ϊ��M��
��Rt��AEF��AE=AF=
��
��EF=
��AM=
EF=
��
��Rt��OBC��OC=2��OB=4����BC=2
��
�ߡ�BOC=��BMA=90�㣬��OBC=��OBM��
���BOC����BMA��
��
=
��
��AB=
��
��OA=OB-AB=4-
��
���A��������-4+
��0������11�֣�
��Բ��A�ڵ�B�����ʱ����Բ��ΪA�䣬����A����A��M���BC�ڵ�M�䣬�ɵã�
��A��M��B�ա�AMB��A��B=AB=
��
��OA��=OB+A��B=4+
��
���A���������-4-
��0����
������������A��������-4+
��0����-4-
��0������13�֣�

| 5 |
��Rt��AOC��AC=
| 5 |
���C��������0��2����
������BC�Ľ���ʽΪy=kx+b��������C��0��2����B��-4��0����
����
|
|
��y=
| 1 |
| 2 |
��2����ͼ1��ʾ�����G������Ϊ��a��c��������G��GH��x�ᣬ����ΪH�㣬
��OH=a��GH=c=
| 1 |
| 2 |
����AP��AG��
��ΪAC=AP��AG=AG������Rt��ACG��Rt��APG��HL����
���ԡ�AGC=
| 1 |
| 2 |
��Rt��ACG�У���AGC=60�㣬AC=
| 5 |
��sin60��=
| AC |
| AG |
2
| ||
| 3 |
��Rt��AGH��AH=OH-OA=a-1��GH=
| 1 |
| 2 |
��AH2+GH2=AG2��
�ࣨa-1��2+(
| 1 |
| 2 |
2
| ||
| 3 |
��֮�ã�a1=
2
| ||
| 3 |
2
| ||
| 3 |
���G��������
2
| ||
| 3 |
| ||
| 3 |
 ��3����ͼ2��ʾ�����ƶ������У����ڵ�A��ʹ��AEFΪֱ�������Σ���9�֣�
��3����ͼ2��ʾ�����ƶ������У����ڵ�A��ʹ��AEFΪֱ�������Σ���9�֣�Ҫʹ��AEFΪֱ�������Σ���AE=AF��
���AEF=��AFE��90�㣬��ֻ���ǡ�EAF=90�㣻
��Բ��A�ڵ�B���Ҳ�ʱ������A��AM��BC������Ϊ��M��
��Rt��AEF��AE=AF=
| 5 |
��EF=
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
��Rt��OBC��OC=2��OB=4����BC=2
| 5 |
�ߡ�BOC=��BMA=90�㣬��OBC=��OBM��
���BOC����BMA��
��
| OC |
| AM |
| BC |
| AB |
��AB=
| 5 |
| 2 |
| 2 |
��OA=OB-AB=4-
| 5 |
| 2 |
| 2 |
���A��������-4+
| 5 |
| 2 |
| 2 |
��Բ��A�ڵ�B�����ʱ����Բ��ΪA�䣬����A����A��M���BC�ڵ�M�䣬�ɵã�
��A��M��B�ա�AMB��A��B=AB=
| 5 |
| 2 |
| 2 |
��OA��=OB+A��B=4+
| 5 |
| 2 |
| 2 |
���A���������-4-
| 5 |
| 2 |
| 2 |
������������A��������-4+
| 5 |
| 2 |
| 2 |
| 5 |
| 2 |
| 2 |


��ϰ��ϵ�д�
�����Ŀ
 ��E����BE=BDʱ�����A�Ķ�����
��E����BE=BDʱ�����A�Ķ�����


 AC��F��
AC��F��


