题目内容
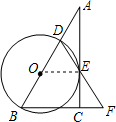
在Rt△ABC中，∠ACB=90°，BD是⊙O的直径，弦DE与AC交于点E，且BD=BF．
（1）求证：AC是⊙O的切线；
（2）若BC=6，AD=4，求⊙O的面积．
（1）求证：AC是⊙O的切线；
（2）若BC=6，AD=4，求⊙O的面积．
（1）证明：连接OE，
∵BD=BF，
∴∠BDF=∠F，
∵OD=OE，
∴∠BDF=∠OED，
∴∠OED=∠F，
∴OE∥BC，
∵在Rt△ABC中，∠ACB=90°，
∴∠OEA=90°，
即OE⊥AC，
∴AC是⊙O的切线；
（2）设半径为x，
∵OE∥BC，
∴△AOE∽△ABC，
∴
=
，
∵BC=6，AD=4，
∴AO=4+x，AB=4+2x，
∴
=
，
解得：x=4或x=-3（舍去）．
∴⊙O的面积为：16π．
∵BD=BF，
∴∠BDF=∠F，
∵OD=OE，
∴∠BDF=∠OED，
∴∠OED=∠F，
∴OE∥BC，
∵在Rt△ABC中，∠ACB=90°，
∴∠OEA=90°，
即OE⊥AC，
∴AC是⊙O的切线；
（2）设半径为x，
∵OE∥BC，
∴△AOE∽△ABC，
∴
| AO |
| AB |
| OE |
| BC |
∵BC=6，AD=4，
∴AO=4+x，AB=4+2x，
∴
| 4+x |
| 4+2x |
| x |
| 6 |
解得：x=4或x=-3（舍去）．
∴⊙O的面积为：16π．
练习册系列答案
相关题目
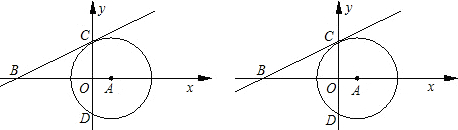
A是线段BO上一动点，连接AD交⊙O于G，过点A作AD的垂线交直线m于点F，交⊙O于点H，连接GH交BC于E．
半径为r．