题目内容
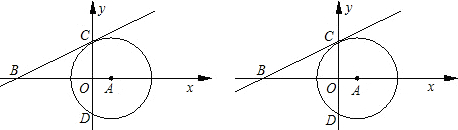
已知：如图，AB是⊙O的直径，PB与⊙O相切于B点，C为⊙O上的点，OP∥AC．试判断PC与⊙O的位置关系，并证明你的结论．
（1）直线PC与⊙O相切．理由如下：
连接OC．
∵AC∥OP，
∴∠1=∠2，∠3=∠4．
∵OA=OC，
∴∠1=∠3．
∴∠2=∠4．
∵在△POC与△POA中，
，
∴△POC≌△POA（SAS），
∴∠PCO=∠PBO．
∵PB切⊙O于点B，AB是⊙O的直径，
∴∠PBO=90°，
∴∠PCO=90°，
∴PC与⊙O相切．
连接OC．
∵AC∥OP，
∴∠1=∠2，∠3=∠4．
∵OA=OC，
∴∠1=∠3．
∴∠2=∠4．
∵在△POC与△POA中，
|
∴△POC≌△POA（SAS），
∴∠PCO=∠PBO．
∵PB切⊙O于点B，AB是⊙O的直径，
∴∠PBO=90°，
∴∠PCO=90°，
∴PC与⊙O相切．
练习册系列答案
名校课堂系列答案
相关题目
半径为r．