Question

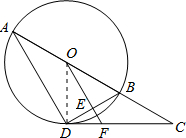
如图，C是⊙O的直径AB延长线上一点，点D在⊙O上，且∠A=30°，∠BDC=

1

2

∠ABD．
（1）求证：CD是⊙O的切线；
（2）若OF∥AD分别交BD、CD于E、F，BD=2，求OE及CF的长．

Answer 1

（1）证明：连接OD．
∵AB是⊙O的直径，
∴∠ADB=90°．
∵∠A=30°，∴∠ABD=60°．
∴∠BDC=

1

2

∠ABD=30°．
∵OD=OB，
∴△ODB是等边三角形．
∴∠ODB=60°．
∴∠ODC=∠ODB+∠BDC=90°．
即OD⊥DC．
∴CD是⊙O的切线；

（2）∵OF∥AD，∠ADB=90°，
∴OF⊥BD，∠BOE=∠A=30°．
∴DE=BE=

1

2

BD=1．
在Rt△OEB中，OB=2BE=2，OE=

OB2-BE2

=

3

．
∵OD=OB=2，∠C=∠ABD-∠BDC=30°，∠DOF=30°，
∴CD=2

3

，DF=OD•tan30°=

2 3

3

．
∴CF=CD-DF=2

3

-

2 3

3

=

4 3

3

．