Question

在△ABC中，分别以AB、BC为直径的⊙O₁、⊙O₂，交于另一点D．
（1）证明：交点D必在AC上；
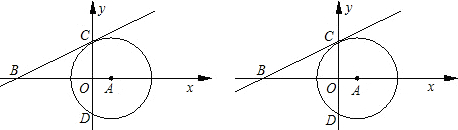
（2）如图甲，当⊙O₁与⊙O₂半径之比为4：3，且DO₂与⊙O₁相切时，判断△ABC的形状，并求tan∠O₂DB的值；
（3）如图乙，当⊙O₁经过点O₂，AB、DO₂的延长线交于E，且BE=BD时，求∠A的度数．

Answer 1

（1）证明：∵AB为⊙O₁的直径，
∴∠ADB=90°，同理∠BDC=90°，
∴∠ADC=180°，
∴点D在AC上．

（2）如图甲，△ABC是以∠B为直角的直角三角形．理由如下：
连接O₁D，O₁O₂．
∵DO₂是⊙O₁的切线，O₁D是半径，
∴∠O₁DO₂=90°，
∵O₁D=O₁B，O₂D=O₂B，O₁O₂公共，
∴△O₁BO₂≌△O₁DO₂，
∴∠O₁BO₂=∠O₁DO₂=90°，
∴△ABC为直角三角形．
又∵BD⊥AC，
∴∠O₂DB=∠O₂BD=∠A，
∴tan∠O₂DB=tan∠A=

BC

AB

=

3

4

．

（3）如图乙，连接O₁O₂，则AC=2O₁O₂=AB；
令∠O₂BD=x，则∠O₂BD=∠O₂DB=x，
∵BD=BE，
∴∠E=x，
∴∠ABD=∠E+∠BDE=2x，∠ACB=∠ABC=3x；
∵BC为⊙O₂直径，
∴∠DBC+∠C=4x=90°，
∴∠A=180°-6x=45°．