题目内容
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,与边AC交于点E,过点D作DF⊥ AC于F.
AC于F.
(1)求证:DF为⊙O的切线;
(2)若DE=
,AB=
,求AE的长.
 AC于F.
AC于F.(1)求证:DF为⊙O的切线;
(2)若DE=
| ||
| 2 |
| 5 |
| 2 |
(1)证明:连接AD,OD;
∵AB为⊙O的直径,
∴∠ADB=90°,
即AD⊥BC;
∵AB=AC,
∴BD=DC.
∵OA=OB,
∴OD∥AC.
∵DF⊥AC,
∴DF⊥OD.
∴∠ODF=∠DFA=90°,
∴DF为⊙O的切线.
(2)连接BE交OD于G;
∵AC=AB,AD⊥BC,ED=BD,
∴∠EAD=∠BAD.
∴
=
.
∴ED=BD,OE=OB.
∴OD垂直平分EB.
∴EG=BG.
又AO=BO,
∴OG=
AE.
在Rt△DGB和Rt△OGB中,
BD2-DG2=BO2-OG2
∴(
)2-(
-OG)2=BO2-OG2
解得:OG=
.
∴AE=2OG=
.

∵AB为⊙O的直径,
∴∠ADB=90°,
即AD⊥BC;
∵AB=AC,
∴BD=DC.
∵OA=OB,
∴OD∥AC.
∵DF⊥AC,
∴DF⊥OD.
∴∠ODF=∠DFA=90°,
∴DF为⊙O的切线.
(2)连接BE交OD于G;
∵AC=AB,AD⊥BC,ED=BD,
∴∠EAD=∠BAD.
∴
 |
| ED |
 |
| BD |
∴ED=BD,OE=OB.
∴OD垂直平分EB.
∴EG=BG.
又AO=BO,
∴OG=
| 1 |
| 2 |
在Rt△DGB和Rt△OGB中,
BD2-DG2=BO2-OG2
∴(
| ||
| 2 |
| 5 |
| 4 |
解得:OG=
| 3 |
| 4 |
∴AE=2OG=
| 3 |
| 2 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
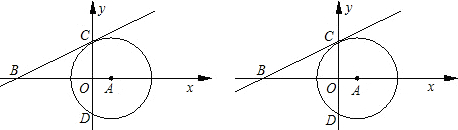
 点D,E为CH的中点,连接AE并延长交BD于F,直线CF交直线AB于点G.
点D,E为CH的中点,连接AE并延长交BD于F,直线CF交直线AB于点G.
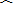




 A是线段BO上一动点,连接AD交⊙O于G,过点A作AD的垂线交直线m于点F,交⊙O于点H,连接GH交BC于E.
A是线段BO上一动点,连接AD交⊙O于G,过点A作AD的垂线交直线m于点F,交⊙O于点H,连接GH交BC于E.