题目内容
【题目】如图,在△ABC中,AB=AC=3,∠B=50°,点D在BC边上(不与点B,C重合),连接AD,作∠ADE=50°,DE交边AC于点E.
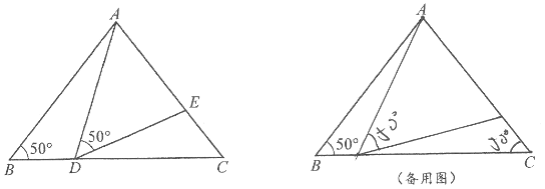
(1)当∠BAD=20°时,求∠CDE的度数;
(2)当CD等于多少时,△ABD≌△DCE?为什么?
(3)在点D运动的过程中,△ADE可能是等腰三角形吗?若可能,直接写出∠DAE的度数;若不可能,说明理由.
【答案】(1)20°;(2)见解析;(3)见解析.
【解析】
(1)利用邻补角的性质和三角形内角和定理解题;
(2)当CD=3时,利用∠B+∠BAD=∠ADE+∠CDE,求出∠BAD=∠CDE,再利用AB=CD=3,∠B=∠C=50°,即可得出△ABD≌△DCE;
(3)△ADE为等腰三角形有三种情况,∠ADE=∠DAC或者∠DAC=∠AED或者∠ADE=∠AED,根据题意排除∠ADE=∠AED的可能.
解:(1)∵∠ADC为三角形ABD的外角.
∴∠B+∠BAD=∠ADE+∠CDE.
∴50°+20°=50°+∠CDE.
∴∠CDE=20°;
(2)CD=3时,△ABD≌△DCE,求证如下:
AB=CD=3,
∵∠B+∠BAD=∠ADE+∠CDE,
由题意知∠B=∠ADE=50°,
∴∠BAD=∠CDE,
又∵AB=AC,△ABC为等腰三角形,
∴∠B=∠C=50°,
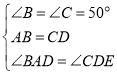 ,
,
∴△ABD≌△DCE(SAS);
(3)△ADE为等腰三角形有三种情况,∠ADE=∠DAC或者∠DAC=∠AED或者∠ADE=∠AED,根据题意排除∠ADE=∠AED的可能,
∵∠C=50°,∠AED肯定大于∠C,
当∠DAE的度数为50°时,
∠BAC=180°-∠B-∠C=80°,
∠BAD=∠CDE=80°-50°=30°,
∠AED=∠C+∠CDE=50°+30°=80°,
∴△ADE的形状是等腰三角形;
∠DAE的度数为65°时,
∠BAD=∠CDE=80°-65°=15°,
∠AED=∠C+∠CDE=50°+15°=65°,
∴△ADE的形状是等腰三角形;
∴三角形ADE为等腰三角形,∠DAE的度数为50°或65°.

【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索,画函数![]() 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:
| …… | -3 | -2 | -1 | 0 | 1 | 2 | 3 | …… |
| …… | 6 | 4 | 2 | 0 | 2 | 4 | 6 | …… |
经历同样的过程画函数![]() 和
和![]() 的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.
的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.
![]() 请直接写出
请直接写出![]() 与
与![]() 的交点坐标和函数
的交点坐标和函数![]() 的对称轴;
的对称轴;
![]() 在所给的平面直角坐标系内画出函数
在所给的平面直角坐标系内画出函数![]() 的图象(不列表),并写出函数
的图象(不列表),并写出函数![]() 的一条性质;
的一条性质;
![]() 结合函数图像,直接写出不等式
结合函数图像,直接写出不等式![]() 时
时![]() 的取值范围.
的取值范围.