题目内容
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y=![]() 在第一象限内的图像交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图像交于点A(m,2),将直线y=2x向下平移后与反比例函数y=![]() 在第一象限内的图像交于点P,且△POA的面积为2.
在第一象限内的图像交于点P,且△POA的面积为2.
(1)求k的值;
(2)求平移后的直线的函数解析式.
【答案】(1) k=2(2)y=2x-4
【解析】试题分析:(1)由点A的纵坐标求得m,即点A的坐标,把点A的坐标代入反比例函数中即可;(2)先求出PM,再求出BN然后用锐角三角函数求出OB,即可.
试题解析:(1)∵点A(m,2)在直线y=2x上,
∴2=2m,
∴m=1,
∴点A(1,2),
∵点A(1,2)在反比例函数y=![]() 上,
上,
∴k=2,
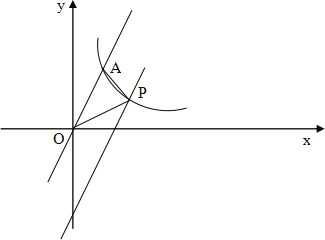
(2)如图,
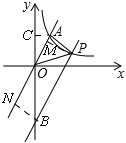
设平移后的直线与y轴相交于B,过点P作PM⊥OA,BN⊥OA,AC⊥y轴
由(1)知,A(1,2),
∴OA=![]() ,sin∠BON=sin∠AOC=
,sin∠BON=sin∠AOC=![]() ,
,
∵S△POA=![]() OA×PM=
OA×PM=![]() ×
×![]() PM=2,
PM=2,
∴PM=![]() ,
,
∵PM⊥OA,BN⊥OA,
∴PM∥BN,
∵PB∥OA,
∴四边形BPMN是平行四边形,
∴BN=PM=![]() ,
,
∵sin∠BON=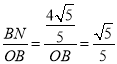 ,
,
∴OB=4,
∵PB∥AO,
∴B(0,4),
∴平移后的直线PB的函数解析式y=2x4.

练习册系列答案
相关题目