��Ŀ����
����Ŀ������ͼ����̽���������������зdz���Ҫ�����ã��������Ǿ�һ������ĺ���չ��̽����������![]() ��ͼ������������ʽ���б�����㡢���߹��̵õ�����ͼ������ͼ��ʾ��
��ͼ������������ʽ���б�����㡢���߹��̵õ�����ͼ������ͼ��ʾ��
| ���� | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ���� |
| ���� | 6 | 4 | 2 | 0 | 2 | 4 | 6 | ���� |
����ͬ���Ĺ��̻�����![]() ��
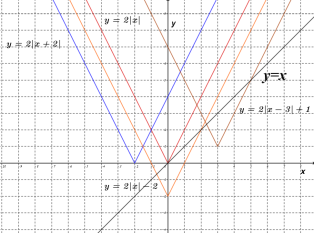
��![]() ��ͼ������ͼ��ʾ���۲췢�֣�����������ͼ����������������ɵ���Գ�ͼ�Σ�������������ʽ�о���ֵǰ���ϵ����ͬ����ͼ��Ŀ��ڷ������״��ȫ��ͬ��ֻ����ߵ�ͶԳ��ᷢ���˱仯��
��ͼ������ͼ��ʾ���۲췢�֣�����������ͼ����������������ɵ���Գ�ͼ�Σ�������������ʽ�о���ֵǰ���ϵ����ͬ����ͼ��Ŀ��ڷ������״��ȫ��ͬ��ֻ����ߵ�ͶԳ��ᷢ���˱仯��
![]() ��ֱ��д��
��ֱ��д��![]() ��
��![]() �Ľ�������ͺ���
�Ľ�������ͺ���![]() �ĶԳ��
�ĶԳ��
![]() ��������ƽ��ֱ������ϵ�ڻ�������
��������ƽ��ֱ������ϵ�ڻ�������![]() ��ͼ��(���б�)����д������
��ͼ��(���б�)����д������![]() ��һ�����ʣ�
��һ�����ʣ�
![]() ��Ϻ���ͼ��ֱ��д������ʽ
��Ϻ���ͼ��ֱ��д������ʽ![]() ʱ
ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��

���𰸡���1����������Ϊ����1��2�����Գ���Ϊֱ��x����2����2��ͼ������������ʣ�����![]() ��ͼ��ĶԳ���Ϊֱ��x��3���𰸲�Ψһ������3��
��ͼ��ĶԳ���Ϊֱ��x��3���𰸲�Ψһ������3��![]()
��������
��1����������ͼ�ɵõ��𰸣�
��2����������![]() ��ͼ�������ͼ�ɵõ���Ӧ��ͼ�����ʣ�
��ͼ�������ͼ�ɵõ���Ӧ��ͼ�����ʣ�
��3���Ȼ���![]() �ĺ���ͼ����ͨ����
�ĺ���ͼ����ͨ����![]() ������������������꣬��Ϻ���ͼ�ɵõ��𰸣�
������������������꣬��Ϻ���ͼ�ɵõ��𰸣�
�⣺��1����ͼ���֪��![]() ��
��![]() �Ľ�������Ϊ����1��2����
�Ľ�������Ϊ����1��2����
����![]() �ĶԳ���Ϊֱ��x����2��
�ĶԳ���Ϊֱ��x����2��
��2������![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��

���ʣ�����![]() ��ͼ��ĶԳ���Ϊֱ��x��3���𰸲�Ψһ����
��ͼ��ĶԳ���Ϊֱ��x��3���𰸲�Ψһ����
��3������![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
���![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��һ����������Ϊ��5��5����
��һ����������Ϊ��5��5����
��![]() ʱ��
ʱ��![]() ��
��
���![]() ��
��
��![]() ��
��
��![]() ��
��![]() ����һ����������Ϊ��
����һ����������Ϊ��![]() ��
��![]() ����
����
����ͼ���֪������ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��