题目内容
【题目】如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.
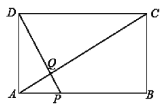
(1)求证:△APQ∽△CDQ;
(2)当PD⊥AC时,求线段PA的长度;
(3)当点P在线段AC的垂直平分线上时,
求sin∠ CPB的值.
【答案】(1)证明见解析;(2)PA=![]() ;(3)sin∠ CPB=
;(3)sin∠ CPB=![]() .
.
【解析】
试题分析:(1)利用两角对应相等的两个三角形易判断△APQ∽△CDQ;(2)由条件可推出△APD∽△DAC,得出![]() ,代入数值可求出PA的值;(3)由勾股定理能够求出PC的长度,再在Rt△CBP中求sin∠ CPB的值.
,代入数值可求出PA的值;(3)由勾股定理能够求出PC的长度,再在Rt△CBP中求sin∠ CPB的值.
试题解析:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠CAB=∠DCA,∠APQ=∠CDQ,∴△APQ∽△CDQ .
(2)PD⊥AC,∴∠ACD+∠PDC=90° ,∵∠PDA+∠PDA=90°,∴∠ACD=∠PDA,∵∠ADC=∠PAD=90°,∴△ADC∽△PDA,∴![]() ,
,![]() ,∴PA=
,∴PA=![]() .(3)当点P在线段AC的垂直平分线上时,PA=PC.设PA=x,则PB=10-x.又在矩形ABCD中,∠B=90°,∴
.(3)当点P在线段AC的垂直平分线上时,PA=PC.设PA=x,则PB=10-x.又在矩形ABCD中,∠B=90°,∴![]() ,∴
,∴![]() .解得:x=
.解得:x=![]() ,∴PC=PA=
,∴PC=PA=![]() .∴sin∠CPB=
.∴sin∠CPB=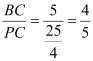

练习册系列答案
相关题目