题目内容
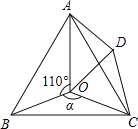
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.
【答案】(1)、证明见解析;(2)、直角三角形、理由见解析;(3)、不能,理由见解析;(4)、α=110°或125°或140°
【解析】
试题分析:(1)、根据△BOC≌△ADC得到OC=DC,结合∠OCD=60°,从而得出等边三角形;(2)、根据△BOC≌△ADC,∠α=150°得到∠ADC=∠BOC=150°,根据等边三角形得到∠ODC=60°,从而得出∠ADO=90°,从而得到三角形的形状;(3)、由△BOC≌△ADC,得∠ADC=∠BOC=∠α,当△AOD为等边三角形时,则∠ADO=60°,结合∠ODC=60°得出∠ADC=120°,又根据∠AOD=∠DOC=60°得出∠AOC=120°,从而求出∠AOC+∠AOB+∠BOC≠360°,从而得到答案;(4)、根据△OCD是等边三角形得到∠COD=∠ODC=60°,根据三角形的性质得出∠ADC=∠BOC=α,∠AOD=190°-α,∠OAD=50°,然后分三种情况分别求出α的大小.
试题解析:(1)、∵△BOC≌△ADC,∴OC=DC.∵∠OCD=60°,∴△OCD是等边三角形.
(2)、△AOD是Rt△.理由如下:
∵△OCD是等边三角形,∴∠ODC=60°, ∵△BOC≌△ADC,∠α=150°,∴∠ADC=∠BOC=∠α=150°,
∴∠ADO=∠ADC-∠ODC=150°-60°=90°,∴△AOD是Rt△.
(3)、不能 理由:由△BOC≌△ADC,得∠ADC=∠BOC=∠α.
若△AOD为等边三角形,则∠ADO=60°,又∠ODC=60°,∴∠ADC=∠α=120°.
又∠AOD=∠DOC=60°,∴∠AOC=120°,又∵∠AOB=110°,
∴∠AOC+∠AOB+∠BOC=120°+120°+110°=350°<360°. 所以△AOD不可能为等边三角形.
(4)、∵△OCD是等边三角形,∴∠COD=∠ODC=60°. ∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°-∠AOB-∠BOC-∠COD=360°-110°-α-60°=190°-α, ∠ADO=∠ADC-∠ODC=α-60°,
∴∠OAD=180°-∠AOD-∠ADO=180°-(190°-α)-(α-60°)=50°.
①当∠AOD=∠ADO时,190°-α=α-60°,∴α=125°.
②当∠AOD=∠OAD时,190°-α=50°,∴α=140°.
③当∠ADO=∠OAD时,α-60°=50°,∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.

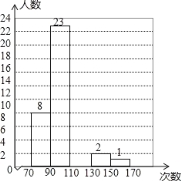
【题目】某校为了了解学生大课间活动的跳绳情况,随机抽取了50名学生每分钟跳绳的次数进行统计,把统计结果绘制成如表和直方图.
次数 | 70≤x<90 | 90≤x<110 | 110≤x<130 | 130≤x<150 | 150≤x<170 |
人数 | 8 | 23 | 16 | 2 | 1 |
根据所给信息,回答下列问题:
(1)本次调查的样本容量是__________;
(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有__________人;
(3)根据上表的数据补全直方图;
(4)如果跳绳次数达到130次以上的3人中有2名女生和一名男生,学校从这3人中抽取2名学生进行经验交流,求恰好抽中一男一女的概率(要求用列表法或树状图写出分析过程).