��Ŀ����
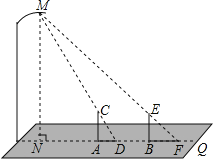
����Ŀ��������С�ֺ�С���������㳡ɢ���������ڵ�����ֱ��NQ�ƶ�����ͼ����С������վ�ڹ㳡��A�㣨��N��5���ש����ʱ����Ӱ��ADǡ��Ϊ1���ש������С������վ�ڹ㳡��B�㣨��N��9���ש����ʱ����Ӱ��BFǡ��Ϊ2���ש������֪�㳡�����ɱ߳�Ϊ0.8�������ε�ש�̳ɣ�С�ֵ�����ACΪ1.6�ף�MN��NQ��AC��NQ��BE��NQ���������������Ϣ�����С������BE�ij����������ȷ��0.01�ף�
���𰸡�С������ԼΪ1.75�ף�
��������
�����������֤����CAD����MND���������������ε��������MN=9.6�ף���֤����EFB����MFN�����ɽ��
�⣺������ã���CAD=��MND=90������CDA=��MDN��
���CAD����MND��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��MN=9.6�ף�
���ߡ�EBF=��MNF=90������EFB=��MFN��
���EFB����MFN��
��![]() =
=![]() ��
��
��![]() =
=![]()
��EB��1.75�ף�
��С������ԼΪ1.75�ף�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ