题目内容
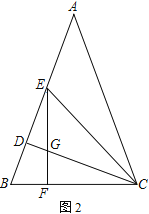
【题目】如图，在Rt△ABC中，∠C=90°，sinA= 
，AB=10，点O为AC上一点，以OA为半径作⊙O交AB于点D，BD的中垂线分别交BD，BC于点E，F，连结DF． 
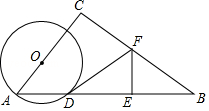
（1）求证：DF为⊙O的切线；
（2）若AO=x，DF=y，求y与x之间的函数关系式．
【答案】
（1）证明：连接OD．
∵OA=OD，
∴∠OAD=∠ODA，
∵EF是BD的中垂线，
∴DF=BF．
∴∠FDB=∠B，
∵∠C=90°，
∴∠OAD+∠B=90°．
∴∠ODA+∠FDB=90°．
∴∠ODF=90°，
又∵OD为⊙O的半径，
∴DF为⊙O的切线
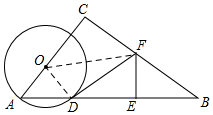
（2）解：连接OF．
在Rt△ABC中，
∵∠C=90°，sinA= 
，AB=10，
∴AC=6，BC=8，
∵AO=x，DF=y，
∴OC=6﹣x，CF=8﹣y，
在Rt△COF中，
OF2=（6﹣x）2+（8﹣x）2
在Rt△ODF中，
OF2=x2+y2
∴（6﹣x）2+（8﹣x）2=x2+y2，
∴y=﹣ 
x+ 
（0＜x≤6）
【解析】（1）连接OD，由于EF是BD的中垂线，DF=BF．从而可知∠FDB=∠B，又因为OA=OD，所以∠OAD=∠ODA，从而可证明∠ODF=90°；（2）连接OF，由题意可知：AO=x，DF=y，OC=6﹣x，CF=8﹣y，然后在Rt△COF中与Rt△ODF中利用勾股定理分别求出OF，化简原式即可求出答案．
【考点精析】利用线段垂直平分线的性质和解直角三角形对题目进行判断即可得到答案，需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
