题目内容
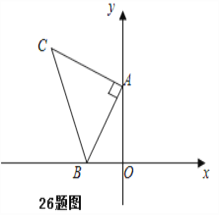
【题目】在△ABC中,AB=AC,CD为AB边上的高
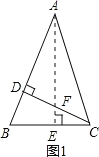
(1) 如图1,求证:∠BAC=2∠BCD
(2) 如图2,∠ACD的平分线CE交AB于E,过E作EF⊥BC于F,EF与CD交于点G.若ED=m,BD=n,请用含有m、n的代数式表示△EGC的面积


【答案】(1)证明见解析;(2)![]() (m+n)m.
(m+n)m.
【解析】
(1) 过A作AE⊥BC于E, 交CD于F, 利用三线合一的性质, 通过证明
∠BAE=∠BCD来证明∠BCD=∠BAE=![]() ∠A;
∠A;
(2) 过点A作AP⊥BC于点P, 求出∠BAP=∠PAC, 求出∠BAP=∠PAC=∠BCD, ∠ACE=∠ECD,推出2 (∠BCD+∠ECD) =90![]() , 求出∠BCE=∠FEC=45
, 求出∠BCE=∠FEC=45![]() , 推出EF=FC, 求出∠BEF=∠BAP=∠BCD, ∠BFE=∠EFC=90
, 推出EF=FC, 求出∠BEF=∠BAP=∠BCD, ∠BFE=∠EFC=90![]() , 根据ASA证出△BFE≌△GFC,得BE=CG=m+n,即可得到结论.
, 根据ASA证出△BFE≌△GFC,得BE=CG=m+n,即可得到结论.
证明:(1)如图1,过A作AE⊥BC于E,交CD于F.
证∠BAE=∠BCD.
∴∠BAC=2∠BCD;
(2)如图2,过点A作AP⊥BC于点P.
∵AB=AC,
∴∠BAP=∠PAC,
∵CD⊥AB,
∴∠CDA=90°
∵CE平分∠DCA,
∴∠ACE=∠ECD,
∴∠ACE+∠PAC=45°
∴∠DCB+∠DCE=45°
∴∠FCE=45°,
∵EF⊥BC,
∴∠EFC=90°
∴EF=FC,
证△BFE≌△GFC(ASA),
∴BE=CG=m+n,
∴△EGC的面积=![]() CGDE=
CGDE=![]() (m+n)m.
(m+n)m.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目