Question

【题目】已知：AC是菱形ABCD的对角线，且AC=BC．

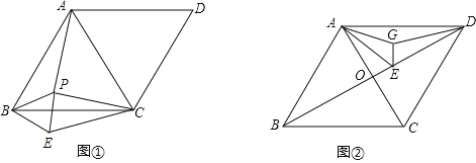
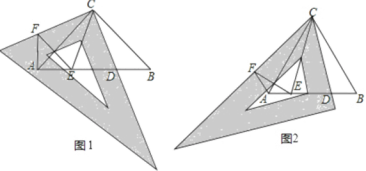
(1)如图①，点P是△ABC的一个动点，将△ABP绕着点B旋转得到△CBE．

①求证：△PBE是等边三角形；

②若BC=5，CE=4，PC=3，求∠PCE的度数；

(2)连结BD交AC于点O，点E在OD上且DE=3，AD=4，点G是△ADE内的一个动点如图②，连结AG，EG，DG，求AG+EG+DG的最小值．

Answer 1

【答案】（1）①见解析，②∠PCE=30°；（2）AG+EG+DG的最小值为5．

【解析】

(1)①先判断出△ABC等边三角形，得出∠ABC=60°，再由旋转知BP=BE，∠PBE=∠ABC=60°，即可得出结论．

②先用勾股定理的逆定理判断出△ACP是直角三角形，得出∠APC=90°，进而判断出∠PBE+∠PCE=90°，即可得出结论；

(2)先判断出△G'DG是等边三角形，得出GG'=DG，即：AG+EG+DG=A'G'+EG+GG'得出当A'、G'、G、E四点共线时，A'G'+EG+G'G的值最小，即可得出结论．

解：(1)①∵四边形ABCD是菱形

∴AB=BC，

∵AC=BC，

∴AB=BC=AC，

∴△ABC等边三角形，

∴∠ABC=60°，

由旋转知BP=BE，∠CBE=∠ABP

∴∠CBE＋∠PBC=∠ABP＋∠PBC

∴∠PBE=∠ABC=60°，

∴△PBE是等边三角形；

②由①知AB=BC=5

∵由旋转知△ABP≌△CBE，

∴AP=CE=4，∠APB=∠BEC，

∵AP2+PC2=42+32=25=AC2，

∴△ACP是直角三角形，

∴∠APC=90°，

∴∠APB+∠BPC=270°，

∵∠APB=∠CEB，

∴∠CEB+∠BPC=270°，

∴∠PBE+∠PCE=360°－（∠CEB+∠BPC）=90°，

∵∠PBE=∠ABC=60°，

∴∠PCE=90°-60°=30°；

(2)如图，将△ADG绕着点D顺时针旋转60°得到△A'DG'，

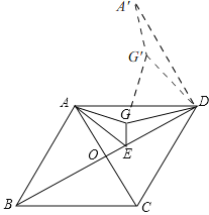
由旋转知△ADG≌△A'DG'，

∴A'D=AD=4，G'D=GD，A'G'=AG，

∵∠G'DG=60°，G'D=GD，

∴△G'DG是等边三角形，

∴GG'=DG，

∴AG+EG+DG=A'G'+EG+GG'

∵当A'、G'、G、E四点共线时，A'G'+EG+G'G的值最小，

即AG+EG+DG的值最小，

∵∠A'DA=60°，∠ADE=∠ADC=30°，

∴∠A'DE=90°，

∴AG+EG+DG=A'G'+EG+G'G=A'E==5，

∴AG+EG+DG的最小值为5．