题目内容
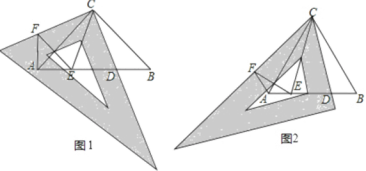
【题目】(1)如图1,△ABC为等腰直角三角形,∠ACB=90°,先将三角板的90°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°).旋转后三角板的一直角边与AB交于点D.在三角板另一直角边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=45°,连接AF,EF.请探究结果:
①直接写出∠EAF的度数=__________度;若旋转角∠BCD=α°,则∠AEF=____________度(可以用含α的代数式表示);
②DE与EF相等吗?请说明理由;
(类比探究)
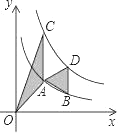
(2)如图2,△ABC为等边三角形,先将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°).旋转后三角板的一直角边与AB交于点D.在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF.
①直接写出∠EAF的度数=___________度;
②若AE=1,BD=2,求线段DE的长度.
【答案】(1)①90,2α;②相等,理由见解析;(2)①120;②![]() .
.
【解析】
(1)①等腰直角三角形的性质可得出AC=BC,∠BAC=∠B=45°,证出∠ACF=∠BCD,由SAS证明出△ACF≌△BCD,得出∠CAF=∠B=45°,AF=DB,即可求解;②证出∠FCE=∠ECD即可证明△CFE≌△CDE,得出EF=DE,∠CFE=∠CDE,从而求出题①中∠AFE的度数;
(2)①由△ABC是等边三角形得出AC=BC,∠BAC=∠B=60°,求出∠ACF=∠BCD,,证明出△ACF≌△BCD,得出∠CAF=∠B=60°即可求解;②证出∠DCE=∠FCE,由SAS证明△CFE≌△CDE,得出DE=EF,作FH⊥AE交EA的延长线于点H,解直角三角形即可求解.
解:(1)①∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,∠BAC=∠B=45°,
∵∠DCF=90°,
∴∠ACF=∠BCD,
在△ACF和△BCD中
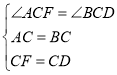
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=45°,AF=DB,
∴∠EAF=∠BAC+∠CAF=90°.
②相等
∵∠ECD=45°,∠FCD=90°,
∴∠FCE=∠ECD =45°,
在△CFE和△CDE中
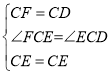
△CFE≌△CDE(SAS),
∴EF=DE,∠CFE=∠CDE,
∵∠CDE=∠B+α°=45°+α°,
∴∠EFC=45°+α°,
∴∠EFC+∠AFE=∠CDB=180°-45°-α,
∴45°+α°+∠AFE=135°-α°,
∴2α°=90°-∠AFE=∠AFE,
∴∠AFE=2α°.
(2)①∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠B=60°,
又∵∠DCF=60°
∴∠ACF=∠BCD,
在△ACF和△BCD中
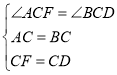
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=60°,
∴∠EAF=∠CAF+∠CAE=120°.
②作FH⊥AE交EA的延长线于点H,如图所示,
∵∠DCF=60°,∠DCE=30°,
∴∠FCE=30°,
∴∠FCE=∠DCE,
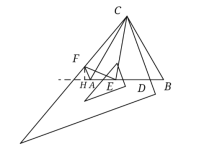
在△CFE和△CDE中
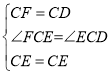
△CFE≌△CDE(SAS),
∴DE=EF,
在Rt△AFH中
∵∠AFH=180°-120°=60°,
∴AF=BD=2,
∴AH=1,FH=![]() ,
,
在Rt△EFH中,EF=![]() ,
,
∴EF=DE=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如图,某项研究表明,大拇指与小拇指尽量张开时,两指尖的距离称为指距.如表是测得的指距与身高的一组数据:
指距d(cm) | 19 | 20 | 21 |
身高h(cm) | 151 | 160 | 169 |
(1)你能确定身高h与指距d之间的函数关系式吗?
(2)若某人的身高为196cm,一般情况下他的指距应是多少?