题目内容
【题目】阅读下面材料：
在数学课上，老师提出如下问题：尺规作图：作已知角的角平分线．已知：如图，∠BAC．求作：∠BAC的角平分线AP．
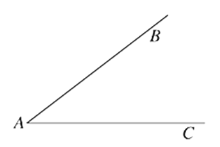
小欣的作法如下：
（1）如图，在平面内任取一点O；
（2）以点O为圆心，AO为半径作圆，交射线AB于点D，交射线AC于点E；
（3）连接DE，过点O作射线OP垂直于线段DE，交⊙O于点P；
（4）过点P作射线AP．
所以射线AP为所求
根据小欣设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明．
证明：∵OP
DE
∴ 
=______（________________________）（填推理的依据），
∴∠BAP=______ （________________________）（填推理的依据）．
【答案】(1)见解析;(2)见解析.
【解析】
（1）根据所述作图即可；
（2）根据垂径定理进行证明回答.
解：（1）作图如下：
（2）
；垂直于弦的直径平分弦，并且平分弦所对的两条弧；∠CAP；等弧所对圆周角相等.
练习册系列答案
相关题目
