Question

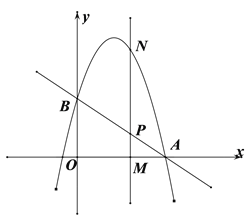
【题目】直线l：y=﹣x+6交y轴于点A，与x轴交于点B，过A、B两点的抛物线m与x轴的另一个交点为C，（C在B的左边），如果BC=5，求抛物线m的解析式，并根据函数图像指出当m的函数值大于0的函数值时x的取值范围．

Answer 1

【答案】x＜3或x＞8

【解析】

试题先根据函数的解析式求出A、B两点的坐标，再求出点C的坐标，利用待定系数法求出抛物线m的解析式，画出其图象，利用数形结合即可求解．

试题解析：∵y=﹣x+6交y轴于点A，与x轴交于点B，

∴x=0时，y=6，

∴A（0，6），

y=0时，x=8，

∴B（8，0），

∵过A、B两点的抛物线m与x轴的另一个交点为C，（C在B的左边），BC=5，

∴C（3，0）．

设抛物线m的解析式为y=a（x﹣3）（x﹣8），

将A（0，6）代入，得24a=6，解得a=，

∴抛物线m的解析式为y=（x﹣3）（x﹣8），即y=x2﹣x+6；

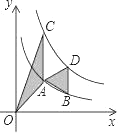
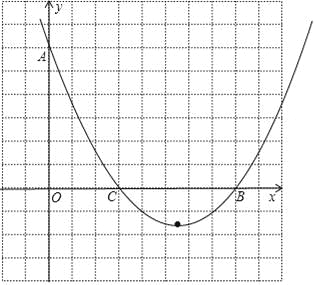
函数图象如右：

当抛物线m的函数值大于0时，x的取值范围是x＜3或x＞8．