题目内容
【题目】下面从认知、延伸、应用三个层面来研究一种几何模型.
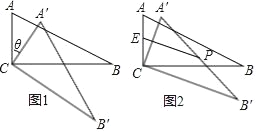
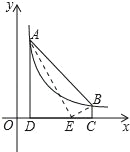
(1)如图,已知点E是线段BC上一点,若∠AED=∠B=∠C.求证 △ABE∽△ECD.

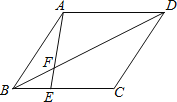
(2)如图,已知点E、F是线段BC上两点,AE与DF交于点H,若∠AHD=∠B=∠C.
求证:△ABE∽△FCD.

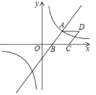
(3)如图,⊙O是等边△ABC的外接圆,点D是![]() 上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点F. 猜想BF、BC、CE三线段的关系,并说明理由.
上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点F. 猜想BF、BC、CE三线段的关系,并说明理由.

【答案】(1)见解析;(2)见解析;(3)BC2=BF×CE.
【解析】
(1)利用△ABE的外角关系证出∠A=∠DEC,又∠B=∠C,从而△ABE∽△ECD;
(2)利用△ABE和△EFH的外角关系证出∠A=∠DFC,又∠B=∠C,从而△ABE∽△FCD;
(3)由圆的内接四边形和等边三角形的性质可知∠BDC=∠CBF=∠ECB=120°,由△CDE的外角关系可得∠E=∠DCB,从而可证△FBC∽△BCE,由相似三角形对应边成比例得出![]() =
=![]() ,从而得到BC2=BF×CE.
,从而得到BC2=BF×CE.
证明:(1)∵∠AEC是△ABE的外角,
∴∠AEC=∠A+∠B,
又∵∠AEC=∠AED+∠DEC,
∴∠A+∠B=∠AED+∠DEC,
∵∠B=∠AED,
∴∠A=∠DEC,
又∵∠B=∠C,
∴△ABE∽△ECD;
(2)∵∠AEC是△ABE的外角,
∴∠AEC=∠A+∠B,
∵∠HEC是△EFH的外角,
∴∠AEC=∠HFE+∠FHE,
∴∠A+∠B=∠HFE+∠FHE,
∵∠B=∠AHD,∠AHD=∠FHE,∴∠B=∠FHE,
∴∠A=∠HFE,
∵∠B=∠C,
∴△ABE∽△FCD;
(3)∵四边形ABDC是⊙O的内接四边形,
∴∠BDC+∠A=180°,
∵△ABC是等边三角形,
∴∠A=∠ACB=∠ABC=60°,
∴∠BDC=∠CBF=∠ECB=120°,
∵∠FDE是△CDE的外角,
∴∠FDE=∠E+∠DCE=120°,
∵∠DCB+∠DCE=120°,
∴∠E=∠DCB,
∴△FBC∽△BCE,
∴![]() =
=![]() ,
,
∴BC2=BF×CE.
故答案为:(1)见解析;(2)见解析;(3)BC2=BF×CE.