Question

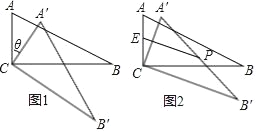
【题目】在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A'B'C．

（1）如图1，当AB∥CB'时，设A'B'与CB相交于点D，求证：△A'CD是等边三角形．

（2）若E为AC的中点，P为A'B'的中点，则EP的最大值是多少，这时旋转角θ为多少度．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）当AB∥CB′时，∠BCB′＝∠B＝∠B′＝30°，则∠A′CD＝90°﹣∠BCB′＝60°，∠A′DC＝∠BCB′+∠B′＝60°，可证：△A′CD是等边三角形；

（2）连接CP，当E、C、P三点共线时，EP最长，根据图形求出此时的旋转角及EP的长．

（1）证明：∵AB∥CB′，

∴∠B＝∠BC B′＝30°，

∴∠BC A′＝90°﹣30°＝60°，

∵∠A′＝∠A＝60°，

∴△A′CD是等边三角形；

（2）如图，连接CP，当△ABC旋转到E、C、P三点共线时，EP最长，

此时θ＝∠ACA1＝120°，

∵∠B′＝30°，∠A′CB′＝90°，

设AC＝a，

∴A′C＝AC＝A′B′＝a，

∵AC中点为E，A′B′中点为P，∠A′CB′＝90°

∴CP＝A′B′＝a，EC＝a，

∴EP＝EC+CP＝a+a＝AC．