题目内容
【题目】如图,点A(m,6),B(n,1)在反比例函数y=![]() 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是( )
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是( )
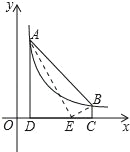
A. (3,0) B. (4,0) C. (5,0) D. (6,0)
【答案】A
【解析】分析:
由题意易得:6m=n,n-m=DC=5,由此即可解得m=1和n=6,设点E的坐标为(x,0),则DE=x-1,CE=6-x,AD=6,BC=1,这样即可由S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE
把S△ABE的面积用含x的代数式表达出来,结合S△ABE=10即可列出关于x的方程,解方程求得x的值即可得到点E的坐标.
详解:
∵点A(m,6),B(n,1)在反比例函数![]() 的图象上,
的图象上,
∴6m=n,n-m=DC=5,
解得:m=1,n=6,
∴点A、B的坐标分别为(1,6)、(6,1),
设点E的坐标为(x,0),则DE=x-1,CE=6-x,
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
连接AE,BE,
则S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE
=![]() (BC+AD)·DC-
(BC+AD)·DC-![]() DE·AD-
DE·AD-![]() CE·BC
CE·BC
=![]()
=![]() .
.
又∵S△ABE=10,
∴![]() ,解得:
,解得:![]() ,
,
∴点E的坐标为(3,0).
故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目