题目内容
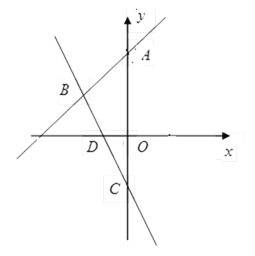
【题目】如图，在平面直角坐标系中，直线AB与直线BC相交于点
，直线AB与
轴相交于点
，直线BC与
轴、轴分别相交于点
、点C．
（1）求直线AB的解析式；
（2）过点A作BC的平行线交轴于点E，求点E的坐标；
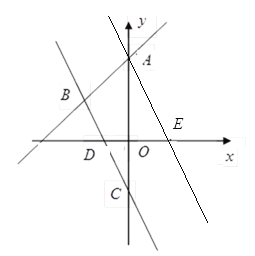
（3）在（2）的条件下，点P是直线AB上一动点且在轴的上方，如果以点D、E、P、Q为顶点的平行四边形的面积等于△ABC，请求出点P的坐标，并直接写出点Q的坐标．
【答案】（1）
；（2）E（2，0）；（3）P(-2，2)，
【解析】
（1）利用待定系数法直接求函数的解析式，（2）先求BC的解析式，利用BC与过A的直线平行与待定系数法求解析式即可，（3）利用△ABC的面积求出点P的纵坐标，再求点P的横坐标，由平行四边形的性质与点的平移得到点Q的坐标．
解：（1）设直线AB过点A(0，4)，
，可设解析式
所以：
，
解得：
所以：直线AB的解析式
（2）设直线BC的解析式为
因为B（-2，2），D（-1，0）
所以
可得
直线BC的解析式为
则过点A且平行于直线BC的解析式为
则E（2，0）
（3）因为：直线BC为：，所以：
，
又因为：
，
所以：
，所以以D、E、P、Q为顶点的平行四边形的面积是6．
如图，由
，
因为：
，
，所以：把代入AB的解析式：，
所以：
，所以
．
因为：
，
所以由平行四边形的性质与点的平移可得：
所以：P(-2，2)，
练习册系列答案
相关题目
