题目内容
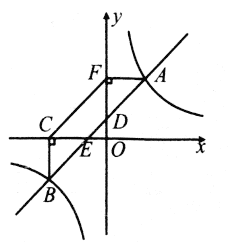
【题目】如图，点A是反比例函数
在第二象限内图象上一点，点B是反比例函数
在第一象限内图象上一点，直线AB与y轴交于点C，且AC＝BC，连接OA、OB，则△AOB的面积是（ ）
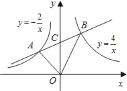
A. 2 B. 2.5 C. 3 D. 3.5
【答案】C
【解析】
分别过A、B两点作x轴的垂线，构成直角梯形，根据AC=BC，判断OC为直角梯形的中位线，得出OD=OE=a，根据双曲线解析式确定A、B两点的坐标及AD、BE的长，根据S△AOB=S梯形ADBE-S△AOD-S△BOE求解．
分别过A、B两点作AD⊥x轴，BE⊥x轴，垂足为D、E，
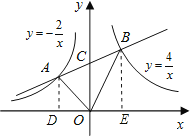
∵AC=CB，
∴OD=OE，
设A（-a，
），则B（a，
），
故S△AOB=S梯形ADBE-S△AOD-S△BOE=
（+）×2a-a×-a×=3．
故选C．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
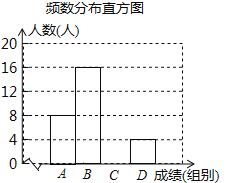
【题目】“品中华诗词，寻文化基因”．某校举办了第二届“中华诗词大赛”，将该校八年级参加竞赛的学生成绩统计后，绘制了如下不完整的频数分布统计表与频数分布直方图．
频数分布统计表
组别 | 成绩x（分） | 人数 | 百分比 |
A | 60≤x＜70 | 8 | 20% |
B | 70≤x＜80 | 16 | m% |
C | 80≤x＜90 | a | 30% |
D | 90≤＜x≤100 | 4 | 10% |
请观察图表，解答下列问题：
（1）表中a= ，m= ；
（2）补全频数分布直方图；
（3）D组的4名学生中，有1名男生和3名女生．现从中随机抽取2名学生参加市级竞赛，则抽取的2名学生恰好是一名男生和一名女生的概率为 ．
