��Ŀ����
����Ŀ��ʮ��������ʿ��ѧ��ŷ��֤���˼������ж�����(V)������(F)������(E)֮����ڵ�һ����Ȥ�Ĺ�ϵʽ������Ϊŷ����ʽ������۲����м��ּĶ�����ģ�ͣ�����������⣺
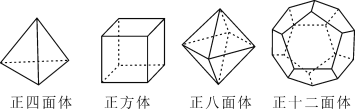
(1)��������Ķ�����ģ�ͣ���ɱ���
������ | ������(V) | ����(F) | ����(E) |
������ | 4 | 4 | |
������ | 8 | 12 | |
�������� | 6 | 8 | 12 |
��ʮ������ | 20 | 12 | 30 |
���Է��ֶ�����(V)������(F)������(E)֮����ڵĹ�ϵʽ��_______________��
(2)��һ��������������ȶ�������8������30���⣬������������������______��
(3)ij��������Ʒ�������Ǽ����壬������������������κͰ˱������ֶ����ƴ�Ӷ��ɣ�����24�����㣬ÿ�����㴦��3���⣮��ö���������������εĸ���Ϊx���˱��εĸ���Ϊy����x��y��ֵ��
���𰸡�(1)6,6,V��F��E��2 ;(2)20;(3)x��y��F��14
��������
��1���ӱ���۲췢�֣�������+����-����=2����2�����루1���е�ʽ�Ӽ��ɵõ���������3���õ�����������������������Ϊx+y��ֵ��
�⣺��1�������������Ϊ6����������Ķ�����Ϊ6����ϵʽΪ��V+F-E=2��
��2��������ã�F-8+F-30=2�����F=20��
��3������24�����㣬ÿ�����㴦����3���⣬����ȷ��һ��ֱ�ߣ�
���24��3��2=36���⣬
��ô24+F-36=2�����F=14��
��x+y=14��
�ʴ�Ϊ��6��6��E=V+F-2��20��14��

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д� �߽�������ϵ�д�
�߽�������ϵ�д�����Ŀ�������������ˮƽ�ߺ���ֱ�߽�ƽ��ֳ����ɸ����Ϊ1��С�����θ��ӣ�С�����εĶ���и�㣬�Ը��Ϊ����Ķ���νи�����Σ��������ε����ΪS���������ϸ��ĸ�����Ϊx��������ڲ��ĸ����Ϊn��S��x��n֮���Ƿ����һ����������ϵ�أ� 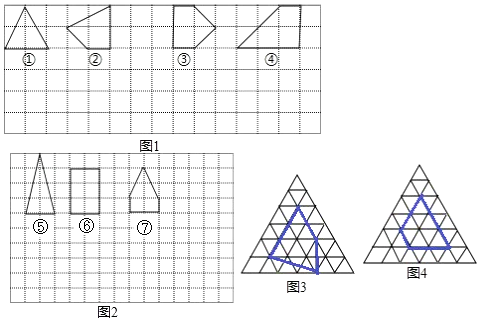
��1������̽����
��ͼ1��ͼ����ʾ�ĸ�����Σ����ڲ���ֻ��һ����㣬���ǵ����������ϸ��ĸ����͵Ķ�Ӧ��ϵ���±�������д�±���д��S��x֮��Ĺ�ϵʽS= ��
������� | �� | �� | �� | �� | �� |
�������S | 2 | 2.5 | 3 | 4 | �� |
�����ϸ��ĸ�����x | 4 | �� |
��2����ͼ2����ʾ�ĸ�����Σ���Щ������ڲ�������ֻ��2����㣮̽����ʱ�����ĸ�������ε����S���������ϸ��ĸ�����x֮��Ĺ�ϵʽS= ��
��3�������̽��������������ڲ�����ֻ��n��n���������������ʱ������S��x��n֮��Ĺ�ϵʽS=���ú�����ĸx��n�Ĵ���ʽ��ʾ��
��4��������չ��
�����������������е������������̽������ͼ3��4����������������ÿ��С�����������Ϊ1��С�������εĶ���Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ�ͼ�Ǹ��������θ���е���������Σ�
����ͼ���ṩ����Ϣ�����
������θ����ϵĸ��ĸ��� | ��������ڲ��ĸ����� | ������ε���� | |
�����1��ͼ3�� | 8 | 1 | 8 |
�����2��ͼ4�� | 7 | 3 | 11 |
�� | �� | �� | �� |
�� | �� | �� | �� |
�� | �� | �� | �� |
һ�������� | a | b | S |
��S��a��b֮��Ĺ�ϵΪS=���ú�a��b�Ĵ���ʽ��ʾ����