��Ŀ����
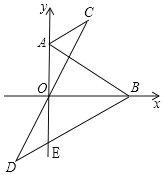
����Ŀ����ƽ��ֱ������ϵ�У���A��0��6����B��8��0����AB=10����ͼ����DBO=��ABO����CAy=��BAO��BD��y���ڵ�E��ֱ��DO��AC�ڵ�C��
��1������֤����ACO�ա�EDO��������߶�AC��BD��λ�ù�ϵ��������ϵ��
��2������P��A��������A��O��B·���˶����ٶ�Ϊ1����B�㴦ֹͣ�˶�������Q��B��������B��O��A�˶����ٶ�Ϊ2����A�㴦ֹͣ�˶�������ͬʱ��ʼ�˶�����Ҫ������Ӧ���յ����ֹͣ����ijʱ�̣���PE��CD�ڵ�E��QF��CD�ڵ�F�����������˶��ʱ��ʱ��OPE���OQFȫ�ȣ�

���𰸡���1��AC��BD��AC=BD��10����2�����������˶�ʱ��Ϊ2��![]() ��12��ʱ����OPE����OQFȫ��.
��12��ʱ����OPE����OQFȫ��.
��������
��1���ٸ���ȫ�������ε��ж�����ASA֤�ý��ۣ�
�����â���ȫ�������ε����ʵõ���AC��BD��AC=BD-10��
��2�����˶���ʱ��Ϊt�룬��i������P��Q�ֱ���y�ᡢx����ʱ��ii������P��Q����y����ʱ����iii������P��x���ϣ�Q��y��ʱ�����߶�û����ǰֹͣ������Q��ǰֹͣʱ���з��̼��ɵõ����ۣ�
��1������ͼ��
�ߡ�DBO=��ABO��OB��AE��
���BAO=��BEO��
��AB=BE��
��AO=OE��
�ߡ�CAy=��BAO��
���CAy=��BEO��
���DEO=��CAO
����ACO����EDO��
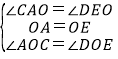 ��
��
���ACO�ա�EDO��ASA����
���ɢ�֪����ACO�ա�EDO��
���C=��D��AC=DE��
��AC��BD��AC=BD��10��
��2�����˶���ʱ��Ϊt�룬
��i������P��Q�ֱ���y�ᡢx����ʱPO=QO�ã�6��t=8��2t�����t=2���룩��
��ii������P��Q����y����ʱPO=QO�ã�6��t=2t��8�����t=![]() ���룩��
���룩��
��iii������P��x���ϣ�Q��y��ʱ�����߶�û����ǰֹͣ����PO=QO�ã�t��6=2t��8�����t=2���룩�������⣻
����Q��ǰֹͣʱ����t��6=6�����t=12���룩��
�������������������˶�ʱ��Ϊ2��![]() ��12��ʱ����OPE����OQFȫ��.
��12��ʱ����OPE����OQFȫ��.

����Ŀ��ʮ��������ʿ��ѧ��ŷ��֤���˼������ж�����(V)������(F)������(E)֮����ڵ�һ����Ȥ�Ĺ�ϵʽ������Ϊŷ����ʽ������۲����м��ּĶ�����ģ�ͣ�����������⣺
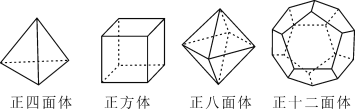
(1)��������Ķ�����ģ�ͣ���ɱ���
������ | ������(V) | ����(F) | ����(E) |
������ | 4 | 4 | |
������ | 8 | 12 | |
�������� | 6 | 8 | 12 |
��ʮ������ | 20 | 12 | 30 |
���Է��ֶ�����(V)������(F)������(E)֮����ڵĹ�ϵʽ��_______________��
(2)��һ��������������ȶ�������8������30���⣬������������������______��
(3)ij��������Ʒ�������Ǽ����壬������������������κͰ˱������ֶ����ƴ�Ӷ��ɣ�����24�����㣬ÿ�����㴦��3���⣮��ö���������������εĸ���Ϊx���˱��εĸ���Ϊy����x��y��ֵ��