题目内容
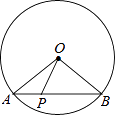
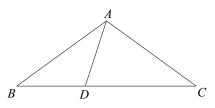
【题目】如图，在△ABC中，D是BC边上一点，AD=BD，AB=AC=CD，求∠BAC的度数.
【答案】108°.
【解析】
试题先设∠B=x，由AB=AC可知，∠C=x，由AD=DB可知∠B=∠DAB=x，由三角形外角的性质可知∠ADC=∠B+∠DAB=2x，根据AB=CD可知∠ADC=∠CAD=2x，再在△ACD中，由三角形内角和定理即可得出关于x的一元一次方程，求出x的值即可．
试题解析：设∠B=x，∵AB=AC，∴∠C=∠B=x，∵AD=DB，∴∠B=∠DAB=x，∴∠ADC=∠B+∠DAB=2x，∵AB=CD，∴∠ADC=∠CAD=2x，在△ACD中，∠C=x，∠ADC=∠CAD=2x，∴x+2x+2x=180°，解得x=36°．∴∠ABC=36°．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单的多面体模型，解答下列问题：
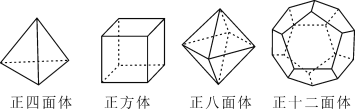
(1)根据上面的多面体模型，完成表格：
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
正方体 | 8 | 12 | |
正八面体 | 6 | 8 | 12 |
正十二面体 | 20 | 12 | 30 |
可以发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______________；
(2)若一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是______；
(3)某个玻璃饰品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处有3条棱．设该多面体外表面三角形的个数为x，八边形的个数为y，求x＋y的值．
