ĢāÄæÄŚČŻ
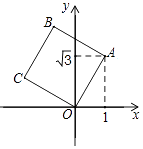
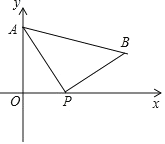
”¾ĢāÄæ”æČēĶ¼£¬A£Ø0£¬4£©ŹĒÖ±½Ē×ų±źĻµ y ÖįÉĻŅ»µć£¬¶Æµć P “ÓŌµć O ³ö·¢£¬ŃŲ x ÖįÕż°ėÖįŌĖ¶Æ£¬ĖŁ¶ČĪŖĆæĆė 1 øöµ„Ī»³¤¶Č£¬ŅŌPĪŖÖ±½Ē¶„µćŌŚµŚŅ»ĻóĻŽÄŚ×÷µČŃüRt”÷APB£®ÉčPµćµÄŌĖ¶ÆŹ±¼äĪŖ t Ćė£®
£Ø1£©Čō AB”Īx Öį£¬Ēó t µÄÖµ£»
£Ø2£©ČōOP=![]() OA£¬ĒóBµćµÄ×ų±ź£®
OA£¬ĒóBµćµÄ×ų±ź£®
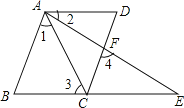
£Ø3£©µ± t=3 Ź±£¬x ÖįÉĻŹĒ·ń“ęŌŚÓŠŅ»µć M£¬Ź¹µĆŅŌ M”¢P”¢A ĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ£¬ĒėÖ±½ÓŠ“³öµć M µÄ×ų±ź£®
”¾“š°ø”æ£Ø1£©4£»£Ø2£©µć B µÄ×ų±źĪŖ£Ø6£¬2£©£»£Ø3£©¼ū½āĪö.
”¾½āĪö”æ
ÓÉ AB”Īx Öį£¬æÉÕŅ³öĖıߊĪ ABCO ĪŖ³¤·½ŠĪ£¬ŌŁøł¾Ż”÷APB ĪŖµČŃüČż½ĒŠĪæɵĆÖŖ”ĻOAP=45”ć£¬“Ó¶ųµĆ³ö”÷AOP ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬ÓÉ“ĖµĆ³ö½įĀŪ£»
×÷ BQ”Ķx ÖįÓŚµć Q£¬Ö¤”÷OAP”Õ”÷QPB µĆ BQ=OP=![]() OA=2£¬PQ=AO=4£¬¾Ż“ĖÖŖ OQ=OP+PQ=6£¬“Ó¶ųµĆ³ö“š°ø£»
OA=2£¬PQ=AO=4£¬¾Ż“ĖÖŖ OQ=OP+PQ=6£¬“Ó¶ųµĆ³ö“š°ø£»
Éčµć M£Øx£¬0£©£¬ÖŖ MA=![]() £¬MP=|x-3|£¬ŌŁ·Ö MA=MP£¬MA=AP£¬ AP=MP ČżÖÖĒéæöĒó½āæÉµĆ£®
£¬MP=|x-3|£¬ŌŁ·Ö MA=MP£¬MA=AP£¬ AP=MP ČżÖÖĒéæöĒó½āæÉµĆ£®
½ā£ŗ£Ø1£©¹żµć B ×÷ BC”Ķx ÖįÓŚµć C£¬ČēĶ¼ 1 ĖłŹ¾£®
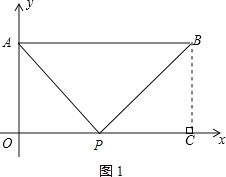
”ßAO”Ķx Öį£¬BC”Ķx Öį£¬ĒŅ AB”Īx Öį£¬
”ąĖıߊĪ ABCO ĪŖ³¤·½ŠĪ£¬
”ąAO=BC=4£®
”ß”÷APB ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąAP=BP£¬”ĻPAB=”ĻPBA=45”ć£¬
”ą”ĻOAP=90”ć-”ĻPAB=45”ć£¬
”ą”÷AOP ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąOA=OP=4£®
t=4”Ā1=4 £ØĆė£©£¬ ¹Ź t µÄÖµĪŖ 4£®
£Ø2£©ČēĶ¼ 2£¬¹żµć B ×÷ BQ”Ķx ÖįÓŚµć Q£¬
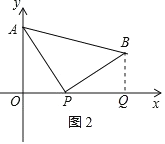
”ą”ĻAOP=”ĻBQP=90”ć£¬
”ą”ĻOAP+”ĻOPA=90”ć£¬
”ß”÷ABP ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąPA=PB£¬”ĻAPB=90”ć£¬
”ą”ĻAOP+”ĻBPQ=90”ć£¬
”ą”ĻOAP=”ĻQPB£¬
”ą”÷OAP”Õ”÷QPB£ØAAS£©£¬
”ą BQ=OP=![]() OA=2£¬PQ=AO=4£¬
OA=2£¬PQ=AO=4£¬
Ōņ OQ=OP+PQ=6£¬
”ąµć B µÄ×ų±źĪŖ£Ø6£¬2£©£»
£Ø3£©µ± t=3 Ź±£¬¼“ OP=3£¬
”ßOA=4£¬
”ąAP=5£¬
Éčµć M£Øx£¬0£©£¬
Ōņ MA=![]() =
=![]() £¬MP=|x-3|£¬
£¬MP=|x-3|£¬
¢Łµ± MA=MP Ź±£¬![]() =|x-3|£¬½āµĆ
=|x-3|£¬½āµĆ
x=-![]() £»
£»
¢Śµ± MA=AP Ź±£¬![]() =5£¬½āµĆ x=-3 »ņ x=3£ØÉį£©£»
=5£¬½āµĆ x=-3 »ņ x=3£ØÉį£©£»
¢Ūµ± AP=MP Ź±£¬|x-3|=5£¬½āµĆ£ŗx=8 »ņ x=-2£»
×ŪÉĻ£¬µć M µÄ×ų±źĪŖ£Ø![]() £¬0£©»ņ£Ø-3£¬0£©»ņ£Ø8£¬0£©»ņ£Ø-2£¬0£©
£¬0£©»ņ£Ø-3£¬0£©»ņ£Ø8£¬0£©»ņ£Ø-2£¬0£©

 Ņ»ĻßĆūŹ¦ĢįÓÅŹŌ¾ķĻµĮŠ“š°ø
Ņ»ĻßĆūŹ¦ĢįÓÅŹŌ¾ķĻµĮŠ“š°ø Ńō¹āŹŌ¾ķµ„ŌŖ²āŹŌ¾ķĻµĮŠ“š°ø
Ńō¹āŹŌ¾ķµ„ŌŖ²āŹŌ¾ķĻµĮŠ“š°ø”¾ĢāÄæ”æŹ®°ĖŹĄ¼ĶČšŹæŹżŃ§¼ŅÅ·ĄÖ¤Ć÷ĮĖ¼ņµ„¶ąĆęĢåÖŠ¶„µćŹż(V)”¢Ćꏿ(F)”¢ĄāŹż(E)Ö®¼ä“ęŌŚµÄŅ»øöӊȤµÄ¹ŲĻµŹ½£¬±»³ĘĪŖÅ·Ą¹«Ź½£®ĒėÄć¹Ū²ģĻĀĮŠ¼øÖÖ¼ņµ„µÄ¶ąĆęĢåÄ£ŠĶ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
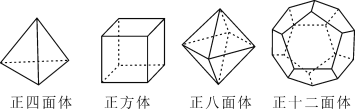
(1)øł¾ŻÉĻĆęµÄ¶ąĆęĢåÄ£ŠĶ£¬Ķź³É±ķøń£ŗ
¶ąĆęĢå | ¶„µćŹż(V) | Ćꏿ(F) | ĄāŹż(E) |
ĖÄĆęĢå | 4 | 4 | |
Õż·½Ģå | 8 | 12 | |
Õż°ĖĆęĢå | 6 | 8 | 12 |
ÕżŹ®¶žĆęĢå | 20 | 12 | 30 |
æÉŅŌ·¢ĻÖ¶„µćŹż(V)”¢Ćꏿ(F)”¢ĄāŹż(E)Ö®¼ä“ęŌŚµÄ¹ŲĻµŹ½ŹĒ_______________£»
(2)ČōŅ»øö¶ąĆęĢåµÄĆꏿ±Č¶„µćŹż“ó8£¬ĒŅÓŠ30ĢõĄā£¬ŌņÕāøö¶ąĆęĢåµÄĆꏿŹĒ______£»
(3)ijøö²£Į§ŹĪĘ·µÄĶāŠĪŹĒ¼ņµ„¶ąĆęĢ壬ĖüµÄĶā±ķĆęŹĒÓÉČż½ĒŠĪŗĶ°Ė±ßŠĪĮ½ÖÖ¶ą±ßŠĪĘ“½Ó¶ų³É£¬ĒŅÓŠ24øö¶„µć£¬Ćæøö¶„µć“¦ÓŠ3ĢõĄā£®ÉčøƶąĆęĢåĶā±ķĆęČż½ĒŠĪµÄøöŹżĪŖx£¬°Ė±ßŠĪµÄøöŹżĪŖy£¬Ēóx£«yµÄÖµ£®