题目内容
【题目】如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是 . 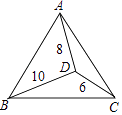
【答案】150°
【解析】解:将△DBC绕点C顺时针旋转60°得△PAC, 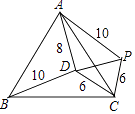
则PC=CD,∠DCP=60°,
∴△CBP为等边三角形,∠PDC=∠PCD=60°,
∵AD=8,BD=10,CD=6,
∴AP=10,PD=CD=6,
∵AD2+DP2=(6)2+(8)2=1002=PA2 ,
∴△ADP是直角三角形,∠ADP=90°,
∴∠ADC=∠ADP+∠PDC=150°.
所以答案是:150°.
【考点精析】根据题目的已知条件,利用勾股定理的逆定理和旋转的性质的相关知识可以得到问题的答案,需要掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单的多面体模型,解答下列问题:
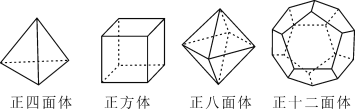
(1)根据上面的多面体模型,完成表格:
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
正方体 | 8 | 12 | |
正八面体 | 6 | 8 | 12 |
正十二面体 | 20 | 12 | 30 |
可以发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______________;
(2)若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是______;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处有3条棱.设该多面体外表面三角形的个数为x,八边形的个数为y,求x+y的值.