题目内容
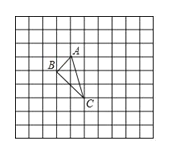
【题目】如图,在△ABC中,∠BAC=90°,射线AM平分∠BAC,AB=8,cos∠ACB= ![]() ,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 .
,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 . 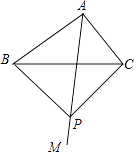
【答案】49
【解析】解:∵在△ABC中,∠BAC=90°,AB=8,cos∠ACB= ![]() , ∴设AC=3k,BC=5k,
, ∴设AC=3k,BC=5k,
∴AB=4k,
∴k=2,
∴BC=10,AC=6,
过P作PE⊥AB于E,PF⊥于F,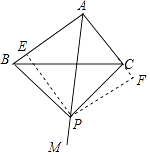
∴四边形AEPF是矩形,
∵射线AM平分∠BAC,
∴PE=PF,
∴矩形AEPF是正方形,
在Rt△PBE与Rt△PFC中 ![]() ,
,
∴Rt△PBE≌Rt△PFC,
∴BE=CF,
∴AE=AF=7,
∴四边形ABPC的面积=正方形AEPF的面积=7×7=49,
所以答案是:49.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.

【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单的多面体模型,解答下列问题:
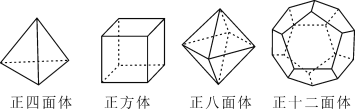
(1)根据上面的多面体模型,完成表格:
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
正方体 | 8 | 12 | |
正八面体 | 6 | 8 | 12 |
正十二面体 | 20 | 12 | 30 |
可以发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______________;
(2)若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是______;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处有3条棱.设该多面体外表面三角形的个数为x,八边形的个数为y,求x+y的值.