Question

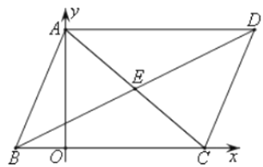
【题目】抛物线y＝x2+bx+c与直线y＝﹣3x交于点A，点A横坐标为n﹣1，其中n＞1，将OA绕点O逆时针旋转90°后形成OB，点B恰好在抛物线上．

（1）求抛物线的解析式（用含n的代数式表示）；

（2）若抛物线与直线y＝﹣x+2n﹣5交于C，D两点，且CD＝2，则m值为多少？

（3）若n为整数，当在x轴下方的抛物线上恰好有5个整数点（横坐标为整数），求出n值．

Answer 1

【答案】（1）y＝x2﹣（4n﹣6）x+3n2﹣11n+8；（2）n＝；（3）n＝﹣1，﹣2，﹣3或3或4．

【解析】

（1）点A在直线y=-3x，则点A（n-1，-3n+3），将OA绕点O逆时针旋转90°后形成OB，由旋转的性质得点B（3n-3，n-1），即可求解；

（2）过D点作x轴的垂线，与过C点作y轴的垂线交于E点，则xC-xD=CD=2，则，则，即可求解；

（3）抛物线在x轴下方恰好有5个整数点，则4＜|x1-x2|＜6，则16＜（|x1-x2|）2＜36，即可求解．

（1）由题意得点A在直线y＝﹣3x，且A点横坐标为n-1,

∴点A（n﹣1，﹣3n+3），

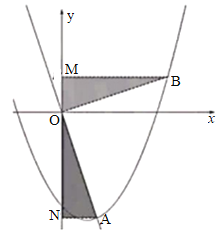
过A，B两点分别向y轴作垂线，垂足分别为N、M，

∴，

∵，

∴，

，

∴B点坐标为（3n-3，n-1），

将A，B两点代入抛物线解析式求得：y＝x2﹣（4n﹣6）x+3n2﹣11n+8；

（2）过D点作x轴的垂线，与过C点作y轴的垂线交于E点，

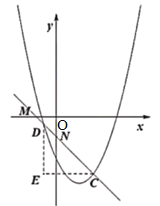
已知直线y＝﹣x+2n﹣5交x轴于M（2n-5,0），交y轴于点N（0，2n-5），

，，，

∵CD＝2，

∴，

∵直线与抛物线相交，

∴，

∴，

∴，

∴，

∴

解得，（舍去）

∴n＝

（3）令y＝0，则y＝x2﹣（4n﹣6）x+3n2﹣11n+8＝0，

则x1+x2＝4n﹣6，x1x2＝3n2﹣11n+8，

∵抛物线在x轴下方恰好有5个整数点，

∴4＜|x1﹣x2|＜6，则16＜（|x1﹣x2|）2＜36，

（|x1﹣x2|）2＝（x1+x2）2﹣4x1x2＝4n2﹣4n+4，

∴3＜n2﹣n＜18，

＜n＜或＜n＜

∵n为整数，

故n＝﹣1，﹣2，﹣3或3或4．