题目内容
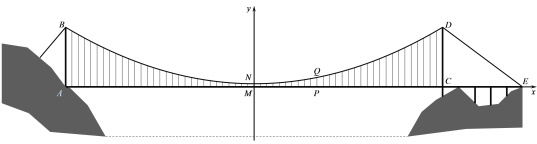
【题目】悬索桥,又名吊桥,指的是以通过索塔悬挂并锚固于两岸(或桥两端)的缆索(或钢链)作为上部结构主要承重构件的桥梁. 其缆索几何形状一般近似于抛物线.从缆索垂下许多吊杆(吊杆垂直于桥面),把桥面吊住.某悬索桥(如图1),是连接两个地区的重要通道. 图2是该悬索桥的示意图.小明在游览该大桥时,被这座雄伟壮观的大桥所吸引. 他通过查找资料了解到此桥的相关信息:这座桥的缆索(即图2中桥上方的曲线)的形状近似于抛物线,两端的索塔在桥面以上部分高度相同,即AB=CD, 两个索塔均与桥面垂直. 主桥AC的长为600 m,引桥CE的长为124 m.缆索最低处的吊杆MN长为3 m,桥面上与点M相距100 m处的吊杆PQ长为13 m.若将缆索的形状视为抛物线,请你根据小明获得的信息,建立适当的平面直角坐标系,求出索塔顶端D与锚点E的距离.


图2
【答案】索塔顶端D与锚点E的距离为155米.
【解析】
先建立适当的平面直角坐标系,AC所在直线为x轴,MN所在直线为y轴,
再由已知条件和抛物线的对称性确定出点坐标:![]() .
.
设抛物线的表达式为![]() .
.
将Q的坐标带入.,解得a的值,就可得出抛物线的表达式.
当MC=![]() 时,带入抛物线的表达式,得出y值就是CD 的长度,在Rt△DCE中利用勾股定理得出DE的长度.
时,带入抛物线的表达式,得出y值就是CD 的长度,在Rt△DCE中利用勾股定理得出DE的长度.
也就是塔顶端D与锚点E的距离
解:如图所示建立平面直角坐标系.
.
依题意可知![]() ,
,
![]() .
.
由抛物线的对称性可知,![]() .则可得点坐标:
.则可得点坐标:![]() .
.
设抛物线的表达式为![]() .
.
因为抛物线经过点Q,
所以将点Q的坐标带入得![]() .
.
解得![]() .
.
得抛物线的表达式为![]() .
.
当![]() 时,得
时,得![]() .
.
因为![]() ,
,
所以![]() .
.
所以![]() .
.
答:索塔顶端D与锚点E的距离为155米.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目