Question

【题目】已知⊙O的半径为4，AB，AC是⊙O的两条条弦，AB＝，点O到AC的距离为，试求出∠BAC的度数.

Answer 1

【答案】15°或75°．

【解析】

根据圆的轴对称性知有两种情况：两弦在圆心的同旁；两弦在圆心的两旁,根据垂径定理和三角函数求解．

解：（1）当圆心O在AB、AC的同一侧时，如图1所示，

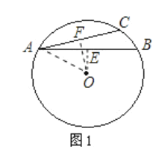
过点O作OE⊥AB于E，OF⊥AC于F，

由垂径定理得，AE=AB=，

在Rt△AOE中，cos∠OAE=，所以∠OAE=30°，

在Rt△AOF中，cos∠OAF=，所以∠OAF=45°，

所以∠BAC=∠OAF-∠OAE=45°-30°=15°．

（2）当圆心O在AB、AC之间时，如图2所示，

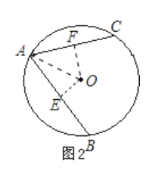
过点O作OE⊥AB于E，OF⊥AC于F，

同样可得，∠OAE=30，∠OAF=45°，

∴∠BAC=∠OAF+∠OAE=45°+30°=75°．

综上所述，∠BAC的度数为15°或75°．