题目内容
【题目】(1)特例求解:在△ABC中,若三角形的三边为6、8、10,则这个三角形的面积 为 .
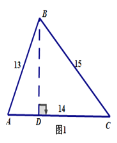
(2)一般化探究:在三角形ABC中,若AB=13,AC=14,BC=15,求△ABC的面积.
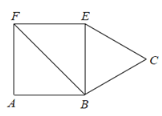
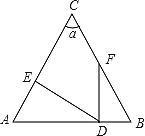
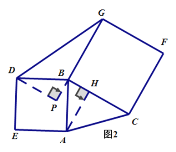
(3)模型建立:在图1三角形中,分别以AB,BC为边向外作正方形ABDE和正方形BCFG,试说明S△ABC=S△BDG.(温馨提示:作DP![]() BG,AH
BG,AH![]() BC)
BC)
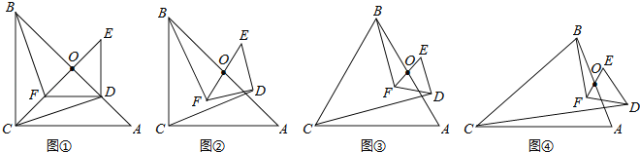
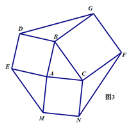
(4)模型应用:分别以图1中三角形的三边为边向外作正方形ABDE、正方形BCFG和正方形AMNC,如图3,利用(3)中的结论求多边形DEMNFG的面积,直接写出结论.
【答案】(1)24;(2)84;(3)见解析;(4)926.
【解析】
(1)先用勾股定理的逆定理判断三角形为直角三角形,再直接直角三角形面积公式求解;
(2)通过作一边上的高将一般三角形转化为直角三角形,利用勾股定理建立方程组计算,即可求解;
(3)先证明![]() ≌
≌![]() (AAS)得到DP=AH,再利用等底等高的三角形面积相等即可得证;
(AAS)得到DP=AH,再利用等底等高的三角形面积相等即可得证;
(4)利用(3)的结论得到![]() =
=![]() =
=![]() =
=![]() ,再结合正方形的面积公式得到多边形DEMNFG的面积=4
,再结合正方形的面积公式得到多边形DEMNFG的面积=4![]() +
+![]() +
+![]() +
+![]() ,从而得解.
,从而得解.
解:(1)∵![]() ,∴△ABC为直角三角形,∴
,∴△ABC为直角三角形,∴![]() ;
;
(2)如图

过点B作BD⊥AC交AC于D,
设AD=x,则DC=14-x,由勾股定理可得:
在直角三角形ADB中,![]() ,
,
在直角三角形BCD中,![]() ,
,
∴![]() ,
,
解得:x=5,
∴![]() ,
,
∴BD=12,
∴![]() ;
;
(3)如图

分别过点D、A作DP![]() BG,AH
BG,AH![]() BC交GB的延长线与P,交BC与H,
BC交GB的延长线与P,交BC与H,
∵∠DBA+∠ABC+∠CBG+∠DBG=360°,而∠DBA=∠CBG=90°,
∴∠ABC+∠DBG=180°,
又∵∠DBP+∠DBG=180°,
∴∠ABC=∠DBP,
在![]() 和
和![]() 中
中

∴![]() ≌
≌![]() (AAS),
(AAS),
∴DP=AH,
又∵![]() ,
,
![]() ,
,
而BC=BG,DP=AH,
∴![]() =
=![]() ;
;
(4)如图

由(3)的证明方法及结论可得:![]() =
=![]() =
=![]() =
=![]() ,
,
而![]() ,
,![]() ,
,![]() ,,
,,
∴多边形DEMNFG的面积=![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]()
=4![]() +
+![]() +
+![]() +
+![]() ,
,
=4×84+![]() +
+![]() +
+![]()
=926

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案