题目内容
【题目】如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,当点H的纵坐标满足条件_________时,∠HOQ<∠POQ.(直接写出答案)

【答案】(1)、A(0,-2);AB=4;(2)、①、t=![]() ;②、-2<
;②、-2<![]() <
<![]() .
.
【解析】
试题分析:(1)、当x=0时求出y的值,即点A的坐标,根据矩形的性质得出点B的坐标,然后求出AB的长度;(2)、①、根据题意得出点A移动的路程,点Q的移动路程;②、当点Q在OA上时,PQ⊥AC,得出△QAP和△ABC相似,从而得出t的值,点Q在OC上时,得出t的值.
试题解析:(1)、抛物线![]() ,当x=0时,y=﹣2,∴A(0,﹣2)由于四边形OABC是矩形,所以AB∥x轴,即A、B的纵坐标相同;当
,当x=0时,y=﹣2,∴A(0,﹣2)由于四边形OABC是矩形,所以AB∥x轴,即A、B的纵坐标相同;当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴B(4,﹣2). ∴AB=4.
(2)、①、由题意知:A点移动路程为AP=t,Q点移动路程为![]() .当Q点在OA上时,即
.当Q点在OA上时,即![]() ,
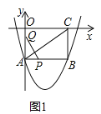
,![]() 时,如图1,若PQ⊥AC, 则有Rt△QAP∽Rt△ABC.∴
时,如图1,若PQ⊥AC, 则有Rt△QAP∽Rt△ABC.∴![]() ,即
,即![]() ,
,
∴![]() .∵
.∵![]() ,∴此时t值不合题意
,∴此时t值不合题意
当Q点在OC上时,即![]() ,
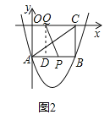
,![]() 时, 如图2,过Q点作QD⊥AB.
时, 如图2,过Q点作QD⊥AB.
∴AD=OQ=7(t﹣1)﹣2=7t﹣9. ∴DP=t﹣(7t﹣9)=9﹣6t.
若PQ⊥AC,则有Rt△QDP∽Rt△ABC,
∴![]() ,即
,即![]() ,∴
,∴![]() .∵
.∵![]() ,∴
,∴![]() 符合题意.
符合题意.
当Q点在BC上时,即![]() ,
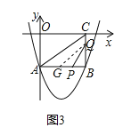
,![]() 时, 如图3,若PQ⊥AC,过Q点作QG∥AC,
时, 如图3,若PQ⊥AC,过Q点作QG∥AC,
则QG⊥PG,即∠GQP=90°. ∴∠QPB>90°.这与△QPB的内角和为180°矛盾,
此时PQ不与AC垂直 综上所述,当![]() 时,有PQ⊥AC.
时,有PQ⊥AC.
②、![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案