Question

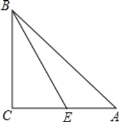
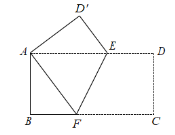
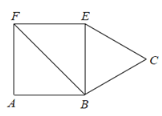
【题目】如图，正方形 ABEF 的面积为 4，△BCE 是等边三角形，点 C 在正方形ABEF 外，在对角线 BF 上有一点 P，使 PC+PE 最小，则这个最小值的平方为（ ）

A.B.C.12D.

Answer 1

【答案】B

【解析】

由于点A与E关于BF对称，所以连接AC，与BF的交点即为P点．此时PC+PE=AC最小，在Rt△ADC中用勾股定理求解即可．

解：连接AE，AC,延长AB,过点C作CD⊥AB于点D,AC与BF交于点P．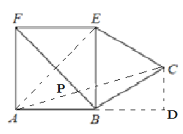

∵点E与A关于BF对称，
∴PA=PE，
∴PC+PE=PA+PE=AC最小．
∵正方形ABCD的面积为4，

∴AB=BE=2，
∵∠CBE=60 ,

∴∠CBD=90 -60 =30 ,

∴CD=BC=1,BD==,
∴AD=2+．
∴在Rt△ADC中，AC2=AD2+CD2=(2+)2+12=

故选：B．