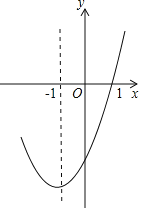题目内容
【题目】已知抛物线y=ax2+bx+c经过(﹣1，0)，(0，﹣3)，(2，3)三点．
（1）求这条抛物线的表达式；
（2）写出抛物线的开口方向、对称轴和顶点坐标．
【答案】（1）y=2x2﹣x﹣3；（2）抛物线的开口向上，对称轴为x=
，顶点坐标为（，﹣
）．
【解析】
（1）将三点代入y=ax2+bx+c，得到三元一次方程组，解方程组即可得到a，b，c的值，从而得到抛物线的解析式．
（2）把解析式化成顶点式，根据抛物线的性质即可得出结论．
解：（1）把(-1,0)，(0,-3)，(2,3)代入y=ax2+bx+c，得
，解得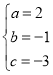
．
所以，这个抛物线的表达式为y=2x2﹣x﹣3．
（2）y=2x2﹣x﹣3=2(x﹣)2﹣，
所以，抛物线的开口向上，对称轴为x=，顶点坐标为（，﹣）
练习册系列答案
津桥教育计算小状元系列答案
相关题目
【题目】“新型冠状病毒肺炎”疫情牵动着亿万国人的心，为进一步加强疫情防控工作，兰州市某学校利用网络平台进行疫情防控知识测试．洪涛同学对九年级1班和2班全体学生的测试成绩数据进行了收集、整理和分析，研究过程中的部分数据如下．
信息一：疫情防控知识测试题共10道题目，每小题10分；
信息二：两个班级的人数均为40人；
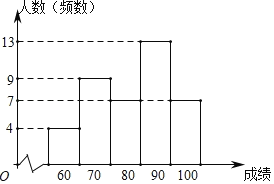
信息三：九年级1班成绩频数分布直方图如图，
信息四：九年级2班平均分的计算过程如下，
80.5(分)；
信息五：
统计量 班级 | 平均数 | 中位数 | 众数 | 方差 |
九年级1班 | 82.5 | m | 90 | 158.75 |
九年级2班 | 80.5 | 75 | n | 174.75 |
根据以上信息，解决下列问题：
（1）m= ，n= ；
（2）你认为哪个班级的成绩更加稳定？请说明理由；
（3）在本次测试中，九年级1班甲同学和九年级2班乙同学的成绩均为80分，你认为两人在各自班级中谁的成绩排名更靠前？请说明理由．
