题目内容
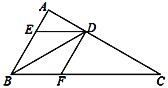
【题目】已知等腰直角![]() ,
,![]() ,
,![]() ,
,![]() 为边
为边![]() 上一动点,连结
上一动点,连结![]() ,在射线
,在射线![]() 上取一点
上取一点![]() 使
使![]() ,若点
,若点![]() 由
由![]() 运动到
运动到![]() ,则点
,则点![]() 运动的路径长为_______.
运动的路径长为_______.
【答案】![]()
【解析】
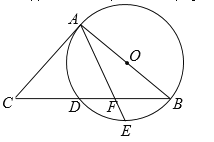
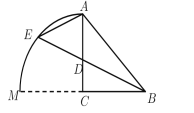
由已知可得△BAD∽△BEA,再结合△ACB是等腰直角三角形,可得∠BEA=45°,以C为圆心,CA为半径画弧交BC延长线于M,根据∠AEB=![]() ∠ACB,可得点E一定落在以C为圆心,CA为半径的圆弧上,即可推出点D由A运动到C,点E走过的路径为弧AM,即可得到答案.
∠ACB,可得点E一定落在以C为圆心,CA为半径的圆弧上,即可推出点D由A运动到C,点E走过的路径为弧AM,即可得到答案.
如图:
∵AB2=BE·BD,
∴![]() ,
,
∵∠ABD=∠EBA,
∴△BAD∽△BEA,
∴∠BAD=∠BEA,
∵△ACB是等腰直角三角形,
∴∠CAB=45°,
∴∠BEA=45°,
以C为圆心,CA为半径画弧交BC延长线于M,
∵∠AEB=![]() ∠ACB,
∠ACB,
∴点E一定落在以C为圆心,CA为半径的圆弧上,
当D与A重合时,E与A重合,
当D与C重合时,E与M重合,
即点D由A运动到C,点E走过的路径为弧AM,
∴弧AM=![]() =
=![]() ,
,
故点E运动的路径长为π,
故答案为:π.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】一般地,对于已知一次函数y1=ax+b,y2=cx+d(其中a,b,c,d为常数,且ac<0),定义一个新函数y=![]() ,称y是y1与y2的算术中项,y是x的算术中项函数.
,称y是y1与y2的算术中项,y是x的算术中项函数.
(1)如:一次函数y1=![]() x﹣4,y2=﹣
x﹣4,y2=﹣![]() x+6,y是x的算术中项函数,即y=
x+6,y是x的算术中项函数,即y= .
.
①自变量x的取值范围是 ,当x= 时,y有最大值;
②根据函数研究的途径与方法,请填写下表,并在图1中描点、连线,画出此函数的大致图象;
x | 8 | 9 | 10 | 12 | 13 | 14 | 16 | 17 | 18 |
y | 0 | 1.2 | 1.6 |
| 2.04 | 2 |
| 1.2 | 0 |

③请写出一条此函数可能有的性质 ;
(2)如图2,已知一次函数y1=![]() x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=
x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y= .
.
①判断:点A、C、E是否在此算术中项函数的图象上;
②在平面直角坐标系中是否存在一点,到此算术中项函数图象上所有点的距离相等,如果存在,请求出这个点;如果不存在,请说明理由.