题目内容
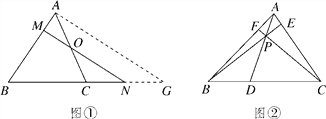
【题目】如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点, ![]() ,求
,求![]() 的值;
的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证: ![]() ;
;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】试题分析:(1)作AG∥MN交BN延长线于点G,证△ABG∽△MBN得![]() ,
,
即![]() ,同理可证△ACG∽△OCN得
,同理可证△ACG∽△OCN得![]() ,结合AO=CO,得NG=CN,从而由
,结合AO=CO,得NG=CN,从而由![]() 进行求解,
进行求解,
(2)由![]() ,
,![]() 可知:
可知: ![]() ,
,
(3)由(2)可知,在△ABD中有![]() , 在△ACD中有
, 在△ACD中有![]() ,
,
从而![]() ,因此可得:
,因此可得: ![]() .
.
(1)解:过点A作MN的平行线交BN的延长线于点G.∵ON∥AG,∴![]() =
=![]() .∵O是AC的中点,∴AO=CO,∴NG=CN.∵MN∥AG,∴
.∵O是AC的中点,∴AO=CO,∴NG=CN.∵MN∥AG,∴![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() .
.
(2)证明:由(1)可知![]() =
=![]() ,
,![]() =
=![]() ,∴
,∴![]() ·
·![]() ·
·![]() =
=![]() ·
·![]() ·
·![]() =1.
=1.
(3)解:在△ABD中,点P是AD上一点,过点P的直线与AB,BD的延长线分别相交于点F,C.由(2)可得![]() ·
·![]() ·
·![]() =1.在△ACD中,过点P的直线与AC,CD的延长线分别相交于点E,B.由(2)可得
=1.在△ACD中,过点P的直线与AC,CD的延长线分别相交于点E,B.由(2)可得![]() ·
·![]() ·
·![]() =1.∴
=1.∴![]() ·
·![]() ·
·![]() =
=![]() ·
·![]() ·
·![]() ,∴
,∴![]() =
=![]() ·
·![]() =
=![]() ×
×![]() =
=![]() .
.

练习册系列答案
相关题目



