题目内容
【题目】已知锐角∠AOB,如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
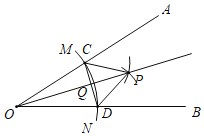
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
【答案】A
【解析】
由作图知OC=OD,CD=CP=DP,根据等边三角形的判定和性质、线段垂直平分线的性质和判定、角平分线的基本作图,逐一判断可得.
由作图可知:射线OP即为∠AOB的角平分线,
∴∠AOP=∠BOP,
故C正确,不符合题意;
由作图(1)(2)可知:OC=OD,CP=DP,
∴OP是CD的垂直平分线,
∴CD⊥OP,
故D正确,不符合题意;
由作图(2)可知:CD=CP=PD,
∴△CDP是等边三角形,
∵CD⊥OP,
∴CP=2CQ,
故B正确,不符合题意;
∵∠AOP=∠BOP,
当OC=CP时,∠AOP=∠CPO,
∴∠CPO=∠BOP,
∴CP∥OB,
故A错误,符合题意;
故选:A.

 作业辅导系列答案
作业辅导系列答案【题目】受到“新型肺炎”影响,全国中小学未能按时开学,为响应国家“停课不停学”的号召,重庆某重点中学组织全校师生开展线上教学活动,体育备课组也为同学们提出了每日锻炼建议.疫情过去开学后,体育组彭老师为检测同学们在家锻炼情况,在甲、乙两班同学中各随机抽取![]() 名学生进行检测,并对数据进行了整理、分析.下面给出了部分信息:
名学生进行检测,并对数据进行了整理、分析.下面给出了部分信息:
甲班![]()
乙班成绩在![]() 中的数据是
中的数据是![]()
整理数据:
成绩 班级 |
|
|
|
|
甲 |
|
|
|
|
乙 |
|
|
|
|
分析数据:
班级 | 平均数 | 中位数 | 众数 |
甲 |
|
|
|
乙 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]()
![]()
![]()
![]() 根据以上数据,你认为哪个班级在家体育锻炼的效果比较好,请说明理由(
根据以上数据,你认为哪个班级在家体育锻炼的效果比较好,请说明理由(![]() 条理由即可).
条理由即可).
![]() 已知九年级共有
已知九年级共有![]() 名学生,请估计全年级体育成绩大于等于
名学生,请估计全年级体育成绩大于等于![]() 分的学生有多少人?
分的学生有多少人?
【题目】一般地,对于已知一次函数y1=ax+b,y2=cx+d(其中a,b,c,d为常数,且ac<0),定义一个新函数y=![]() ,称y是y1与y2的算术中项,y是x的算术中项函数.
,称y是y1与y2的算术中项,y是x的算术中项函数.
(1)如:一次函数y1=![]() x﹣4,y2=﹣
x﹣4,y2=﹣![]() x+6,y是x的算术中项函数,即y=
x+6,y是x的算术中项函数,即y= .
.
①自变量x的取值范围是 ,当x= 时,y有最大值;
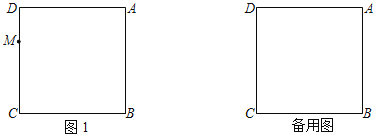
②根据函数研究的途径与方法,请填写下表,并在图1中描点、连线,画出此函数的大致图象;
x | 8 | 9 | 10 | 12 | 13 | 14 | 16 | 17 | 18 |
y | 0 | 1.2 | 1.6 |
| 2.04 | 2 |
| 1.2 | 0 |

③请写出一条此函数可能有的性质 ;
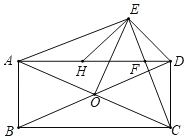
(2)如图2,已知一次函数y1=![]() x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=
x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y= .
.
①判断:点A、C、E是否在此算术中项函数的图象上;
②在平面直角坐标系中是否存在一点,到此算术中项函数图象上所有点的距离相等,如果存在,请求出这个点;如果不存在,请说明理由.