Question

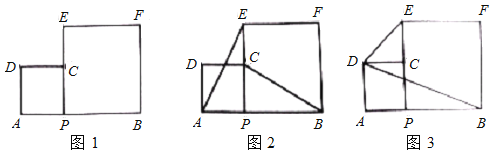
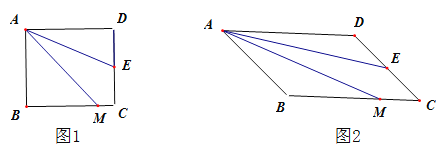
【题目】如图，四边形ABCD是矩形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM.

（1）证明：AM=AD+MC.

（2）若四边形ABCD是平行四边形，其它条件不变，如图，（1）中的结论是否成立？

Answer 1

【答案】（1）见解析；（2）详见解析.

【解析】

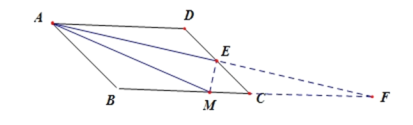
(1)从平行线和中点这两个条件出发，延长AE、BC交于点F，易证Rt△ADE≌Rt△FCE，从而有AD=CF，只需证明AM=MF即可;(2) AM=AD+MC仍然成立，理由为：由四边形ABCD为平行四边形，得到AD与BC平行，利用两直线平行内错角相等得到∠DAE=∠F，再由AE为角平分线得到一对角相等，利用等角对等边得到AM=MF，利用AAS得到三角形ADE与三角形FCE全等，利用全等三角形的对应边相等得到AD=CF，根据AM=MF=AD+MC,即可得证．

（1）延长AE交BC的延长线于点F,

∵E是CD边的中点，

∴DE=EC

∵四边形ABCD是矩形

∴AD//CF

∴∠DAE=∠CFE

又∵AE平分∠DAM

∴∠MAE=∠DAE=∠F

∴AM=MF，

∵∠AED=∠FEC,

∴△ADE≌△FCE（AAS）

∴AD=CF

∴AM=MF=AD+MC;

（2）AM=AD+MC成立，
理由：在平行四边形ABCD中，
∵AD∥BC，
∴∠DAE=∠F，
∵AE平分AE平分∠DAM，
∴∠DAE=∠FAM，
∴∠F=∠FAM，
∴AM=FM，
∵E是CD的中点，
∴DE=CE，
在△ADE和△FCE中，

，
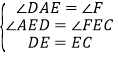∴△ADE≌△FCE（AAS），
∴AD=CF，
∵AM=FM=FC+CM，
∴AM=AD+MC．