题目内容
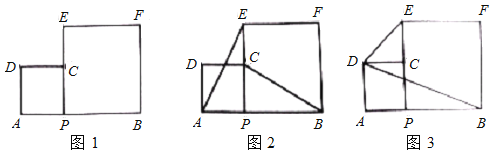
【题目】已知,AB=18,动点P从点A出发,以每秒1个单位的速度向点B运动,分别以AP、BP为边在AB的同侧作正方形。设点P的运动时间为t.
(1)如图1,若两个正方形的面积之和![]() ,
,![]() 当时,求出
当时,求出![]() 的大小;
的大小;
(2)如图2,当![]() 取不同值时,判断直线
取不同值时,判断直线![]() 和
和![]() 的位置关系,说明理由;
的位置关系,说明理由;
(3)如图3,用![]() 表示出四边形
表示出四边形![]() 的面积
的面积![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)由题意,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,然后求出两个正方形面积之和即可;(2)延长
,然后求出两个正方形面积之和即可;(2)延长![]() 交
交![]() 于
于![]() ,根据正方形的性质得到AP=PC,PE=PB,∠APE=∠CPB=90°,在证的△APE≌△PBC,得到
,根据正方形的性质得到AP=PC,PE=PB,∠APE=∠CPB=90°,在证的△APE≌△PBC,得到![]() ,在运用角的运算即可;(3)延长
,在运用角的运算即可;(3)延长![]() ,
,![]() 交于点
交于点![]() ,可得四边形EDBF的面积=四边形HFBA-三角形DEH的面积-三角形ADB的面积,然后根据已知条件和正方形的性质即可解答.
,可得四边形EDBF的面积=四边形HFBA-三角形DEH的面积-三角形ADB的面积,然后根据已知条件和正方形的性质即可解答.
解:(1)由题意,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
(2)![]()
理由如下:
延长![]() 交
交![]() 于
于![]() ,如下图
,如下图

在正方形![]() 和正方形
和正方形![]() 中
中
![]() ,
,![]() ,
,![]() ,
,
![]() 在
在![]() 和
和![]() 中,
中,

![]()
![]() (全等三角形对应角相等)
(全等三角形对应角相等)
![]() ,且
,且![]() ,
,![]() ,
,
![]()
![]() ,即.
,即.![]()
(3)延长![]() ,
,![]() 交于点
交于点![]()

![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图的统计图(图中信息不完整).已知A,B两组捐款人数的比为1∶5.
捐款人数分组统计表
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | x≥40 |
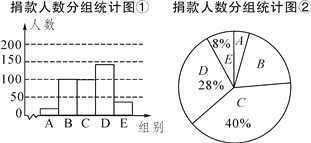
请结合以上信息解答下列问题:
(1)a=____,本次调查的样本容量是______;
(2)先求出C组的人数,再补全“捐款人数分组统计图①;
(3)若该学校自愿捐款的学生有1500人,请估计捐款不少于30元的学生有多少人?