题目内容
【题目】如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
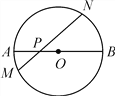
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
(3)若⊙O的半径为R,求PM2+PN2的值.
【答案】(1)MN=2![]() (2)2
(2)2![]() (3)PM2+PN2=2R2
(3)PM2+PN2=2R2
【解析】试题分析:(1)作OH⊥MN于H,连接ON,先计算出![]() ,在Rt△POH中,由于
,在Rt△POH中,由于![]() 则
则![]() 再在Rt△OHN中,利用勾股定理计算出
再在Rt△OHN中,利用勾股定理计算出![]() 然后根据垂径定理由OH⊥MN,得到HM=HN,
然后根据垂径定理由OH⊥MN,得到HM=HN,
所以![]()
(2)作OH⊥MN于H,连接ON,先计算出HM=HN=4,PH=1,在Rt△POH中,由![]() 得到OH=1,再在Rt△OHN中,利用勾股定理可计算出
得到OH=1,再在Rt△OHN中,利用勾股定理可计算出![]()
![]()
(3)作OH⊥MN于H,连接ON,根据垂定理得HM=HN,在Rt△OHN中,利用勾股定理得到![]() 在Rt△POH中,由
在Rt△POH中,由![]() 得
得![]() ,则
,则![]() 然后变形
然后变形![]() 可得到
可得到![]() 所以
所以![]() 的值为
的值为![]()
试题解析:(1)作OH⊥MN于H,连接ON,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,OP=2,
在Rt△POH中,![]()
![]()
在Rt△OHN中,![]()
![]()
∵OH⊥MN,
∴HM=HN,
![]()
(2)作OH⊥MN于H,连接ON,
则HM=HN,
∵MP=3,NP=5,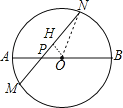
∴MN=8,
∴HM=HN=4,
∴PH=1,
在Rt△POH中, ![]()
∴OH=1,
在Rt△OHN中,∵HN=4,OH=1,
![]()
![]()
(3)作OH⊥MN于H,连接ON,
则HM=HN,
在Rt△OHN中, ![]()
在Rt△POH中, ![]()
∴OH=PH,
∴![]()
![]()

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目