题目内容
【题目】已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,
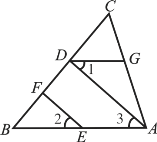
(1)能否得出DG∥BA?试说明理由.(2)EF与BC有什么关系?试说明理由.
【答案】(1)能,DG∥BA,见解析;(2)EF⊥BC,见解析.
【解析】
(1)根据同位角相等,两直线平行,即可得出结论;
(2)先由平行线的性质得到∠1=∠3,又∠1=∠2,所以∠2=∠3,再次推出EF∥AD,即得到∠EFB=∠ADB,已知AD⊥BC于点D,故得到EF与BC的位置关系是垂直.
(1)DG∥BA,
∵∠CDG=∠B(已知),∴DG∥AB(同位角相等,两直线平行),
(2)EF⊥BC
∵∠1=∠3(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠2=∠3,
∴EF∥AD(内同位角相等,两直线平行),
∴∠EFB=∠ADB(两直线平行,同位角相等),
又AD⊥BC于点D(已知),
∴∠ADB=90°,
∴∠EFB=∠ADB=90°,
∴EF⊥CB.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目