题目内容
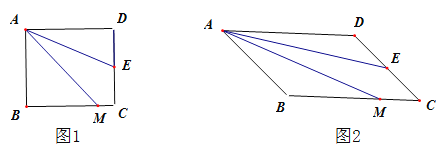
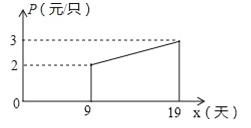
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5![]() ,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.
,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.

【答案】5 ![]()
【解析】
①过D作DP⊥AB于P,,则△ADP是等腰直角三角形,根据等腰直角三角形的性质得到![]() ,进而求得AP=DP=5;
,进而求得AP=DP=5;
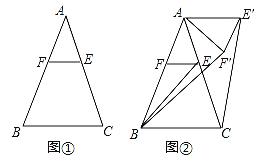
②作点O关于AB的对称点M,点O关于AD的对称点N,连接MN交AB于F交AD于E,则△OEF周长的最小, △OEF周长的最小值=MN,由作图得: AN=AO=AM, ∠NAD=∠DAO, ∠MAB=∠BAO,于是得到![]() .根据三角形的中位线的性质得到
.根据三角形的中位线的性质得到![]() ,
,![]() ,根据勾股定理得到
,根据勾股定理得到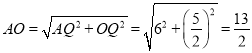 ,然后根据等腰直角三角形的性质即可得到结论.
,然后根据等腰直角三角形的性质即可得到结论.
①过D作DP⊥AB于P,
则A△DP是等腰直角三角形,![]() ,
,
![]() ,
,
∴AP=DP=sin45°×5![]() =5;
=5;
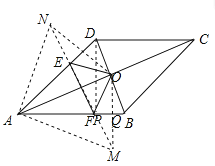
②作点O关于AB的对称点M,点O关于AD的对称点N,连接MN交AB于F交AD于E,则△OEF周长的最小, △OEF周长的最小值=MN,
由作图得:AN=AO=AM, ∠NAD=∠DAO, ∠MAB=∠BAO,
![]() ,
,
![]() ,
,
∵OM⊥AB于Q,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,![]() ,
,
![]()
∴△OEF周长的最小值是![]() .
.
故答案为①5;② ![]() .
.

练习册系列答案
相关题目